Chứng minh rằng nếu G và G' lần lượt là trọng tâm của các tam giác ABC và A'B'C' thì \(3\overrightarrow{GG'}=\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}\) ?
Trong mặt phẳng tọa độ Oxy, các khẳng định sau đúng hay sai ?
a) Hai vectơ đối nhau thì chúng có hoành độ đối nhau
b) Vectơ \(\overrightarrow{a}\ne0\) cùng phương với vectơ \(\overrightarrow{i}\) nếu \(\overrightarrow{a}\) có hoành độ bằng 0
c) Vectơ \(\overrightarrow{a}\) có hoành độ bằng 0 thì cùng phương với vectơ \(\overrightarrow{j}\)
Cho tam giác đều ABCD nội tiếp trong đường tròn O. Hãy xác định các điểm M, N, P sao cho :
a) \(\overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{OB}\)
b) \(\overrightarrow{ON}=\overrightarrow{OB}+\overrightarrow{OC}\)
c) \(\overrightarrow{OP}=\overrightarrow{OC}+\overrightarrow{OA}\)
Cho tam giác OAB. Gọi M và N lần lượt là trung điểm của OA và OB. Tìm các số m, n sao cho :
a) \(\overrightarrow{OM}=m\overrightarrow{OA}+n\overrightarrow{OB}\)
b) \(\overrightarrow{AN}=m\overrightarrow{OA}+n\overrightarrow{OB}\)
c) \(\overrightarrow{MN}=m\overrightarrow{OA}+n\overrightarrow{OB}\)
d) \(\overrightarrow{MB}=m\overrightarrow{OA}+n\overrightarrow{OB}\)
Cho tam giác đều ABC có cạnh bằng a. Tính :
a) \(\left|\overrightarrow{AB}+\overrightarrow{AC}\right|\)
b) \(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|\)
Chứng minh rằng \(\left|\overrightarrow{a}+\overrightarrow{b}\right|\le\left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|\) ?
Cho hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) đều khác \(\overrightarrow{0}\). Các khẳng đinh sau đúng hay sai ?
a) Hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) cùng hướng thì cùng phương
b) Hai vectơ \(\overrightarrow{b}\) và \(k\overrightarrow{b}\) cùng phương
c) Hai vectơ \(\overrightarrow{a}\) và \(-2\overrightarrow{a}\) cùng hướng
d) Hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) ngược hướng với vectơ thứ ba khác \(\overrightarrow{0}\) thì cùng phương
Cho lục giác đều ABCDEF có tâm O. Hãy chỉ ra các vectơ bằng \(\overrightarrow{AB}\) có điểm đầu và điểm cuối là O hoặc các đỉnh của lục giác ?
Tứ giác ABCD là hình gì nếu \(\overrightarrow{AB}=\overrightarrow{CD}\) và \(\left|\overrightarrow{AB}\right|=\left|\overrightarrow{BC}\right|\) ?
Cho 6 điểm M, N, P, Q, R, S bất kì. Chứng minh rằng :
\(\overrightarrow{MP}+\overrightarrow{NQ}+\overrightarrow{RS}=\overrightarrow{MS}+\overrightarrow{NP}+\overrightarrow{RQ}\)
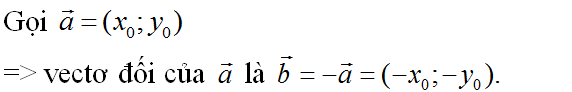
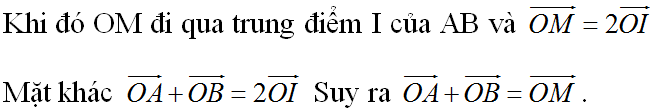
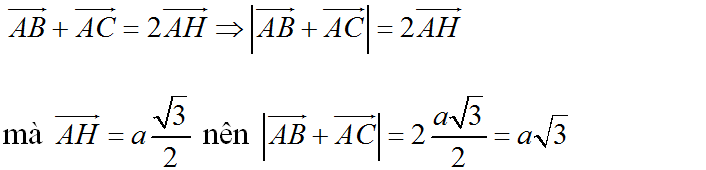
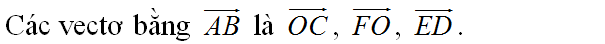
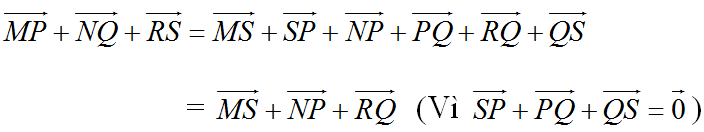
Trả lời bởi Anh Triêt