Chứng minh rằng tứ giác ABCD là một hình bình hành khi và chỉ khi \(\overrightarrow {BC} = \overrightarrow {AD}.\)
Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Hãy chỉ ra tập hợp S gồm tất cả các vecto khác \(\overrightarrow 0 \). Hãy chỉ ra tập hợp S gồm tất cả các vceto khác \(\overrightarrow 0 \), có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O}. Hãy chia tập S thành các nhóm sao cho hai vecto thuộc cùng một nhóm khi và chỉ khi chúng bằng nhau.
Tham khảo:
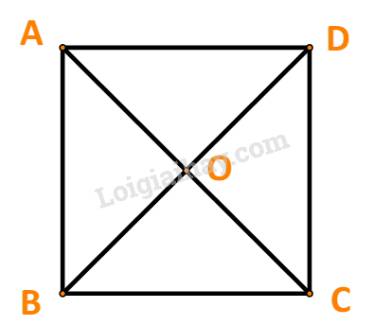
Tập hợp S là: \(S = \{ \overrightarrow {AB} ;\;\overrightarrow {AC} ;\;\overrightarrow {AD} ;\;\overrightarrow {AO} ;\;\overrightarrow {BA} ;\;\overrightarrow {BC} ;\;\overrightarrow {BD} ;\;\overrightarrow {BO} ;\;\overrightarrow {CB} ;\;\overrightarrow {CA} ;\;\overrightarrow {CD} ;\;\overrightarrow {CO} ;\;\overrightarrow {DB} ;\;\overrightarrow {DC} ;\;\overrightarrow {DA} ;\;\overrightarrow {DO} ;\;\overrightarrow {OB} ;\;\overrightarrow {OC} ;\;\overrightarrow {OD} ;\;\overrightarrow {OA} \} \)
Các nhóm trong S là:
\(\begin{array}{l}\{ \overrightarrow {AB} ;\overrightarrow {DC} \} ,\{ \overrightarrow {BA} ;\overrightarrow {CD} \} ,\{ \overrightarrow {AD} ;\overrightarrow {BC} \} ,\{ \overrightarrow {DA} ;\overrightarrow {CB} \} ,\\\{ \overrightarrow {AO} ;\overrightarrow {OC} \} ,\{ \overrightarrow {OA} ;\overrightarrow {CO} \} ,\{ \overrightarrow {OB} ;\overrightarrow {DO} \} ,\{ \overrightarrow {BO} ;\overrightarrow {OD} \} .\end{array}\)
Trả lời bởi Kiều Sơn TùngTrên mặt phẳng tọa độ Oxy hãy vẽ các vecto \(\overrightarrow {OA} ,\;\overrightarrow {MN} \) với A (1; 2), M (0; -1), N (3; 5).
a) Chỉ ra mỗi quan hệ giữa hai vecto trên.
b) Một vật thể khởi hành từ M chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn vởi vecto \(\overrightarrow v = \overrightarrow {OA} \). Hỏi vật thể đó có đi qua N hay không? Nếu có thì sau bao lâu sẽ tới N?
Tham khảo:
a)
Lấy điểm B(0;2) và P(0;5).
Ta có: OB=2, AB =1, MP=6 và PN=3.
Xét hai tam giác vuông OBA và MPN ta có: \(\frac{{OB}}{{MP}} = \frac{{AB}}{{PN}} = \frac{1}{3}\)
Do đó hai tam giác đồng dạng và OA // MN.
Suy ra \(\overrightarrow {OA} ,\;\overrightarrow {MN} \) cùng phương.
Hơn nữa, \(\overrightarrow {OA} ,\;\overrightarrow {MN} \) cùng hướng và MN = 3 OA.
b) Mỗi giờ, vật thể đó đi được quãng đường tương ứng với đoạn thẳng OA.
Vì \({MN} = 3. {OA} \) nên vật thể đó sẽ đi qua N sau 3 giờ kể từ lúc khởi hành.
Trả lời bởi Kiều Sơn Tùng
Tứ giác ABCD là một hình bình hành \( \Leftrightarrow \left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\)
\( \Leftrightarrow \) Hai vecto \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) cùng hướng và AD = BC.
\( \Leftrightarrow \overrightarrow {BC} = \overrightarrow {AD} .\) (đpcm)
Trả lời bởi Hà Quang Minh