BÀI 6: Khái niệm về phép dời hình và hai hình bằng nhau

a)

Gọi r = OA, α là góc lượng giác (Ox, OA), β là góc lượng giác (Ox, OA'). Giả sử A'= ( x'; y'). Khi đó ta có:

β = α -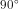 , x = r cos α, y = r sin α

Suy ra:

x' = r cos β = r cos ( α -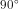 ) = r sinα = y

y' = r sin β = r sin ( α -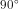 ) = - r cos α= - x

Do đó phép quay tâm O góc -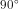 biến A(-3;2) thành A'(2;3). Các trường hợp khác làm tương tự

b)

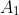
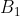
Gọi tam giác 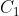là ảnh của tam giác A'B'C' qua phép đối xứng trục Ox. Khi đó 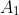(2;-3), 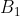(5;-4), 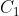(3;-1) là đáp số cần tìm.

Gọi L là trung điểm của đoạn thẳng OF. Ta thấy phép đối xứng qua đường thẳng EH biến hình thang AEJK thành hình thang BELF, phép tịnh tiến theo vectơ BF biến hình thang BELF thành hình thang FOIC. Như vậy phép dời hình có được bằng cách thực hiện liên tiếp phép biến hình trên, sẽ biến hình thang AEJK thành hình thang FOIC. Do đó hai hình thang AEJK và FOIC bằng nhau.

Gọi phép dời hình đó là f. Do f biến các đoạn thẳng AB, AC tương ứng thành các đoạn thẳng A'B', A'C' nên nó cũng biến các trung điểm M, N của các đoạn thẳng AB, AC tương ứng theo thứ tự thành các trung điểm M', N' của các đoạn thẳng A'B', A'C'. Vậy f biến các trung tuyến CM, BN của tam giác ABC tương ứng thành các trung tuyến C'M', B'N' của tam giác A'B'C'. Từ đó suy ra f biến trọng tâm G của tam giác ABC của CM và BN thành trọng tâm G' của tam giác A'B'C' là giao của C'M' và B'N'.

a)
Qua phép đối xứng trục Oy điểm \(M\left(1;1\right)\) biến thành điểm \(M'\left(x;y\right)\) có tọa độ là: \(\left\{{}\begin{matrix}x'=-x=-1\\y'=y=1\end{matrix}\right.\).
Suy ra: \(M'\left(-1;1\right)\).
Qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}\left(2;0\right)\) điểm M' biến thành điểm \(A\left(x_A;y_A\right)\) là:\(\left\{{}\begin{matrix}x_A=-1+2=1\\y_A=0+1=1\end{matrix}\right.\).
Suy ra: \(A\left(1;1\right)\equiv M\) là điểm cần tìm.
b) Gọi C là ảnh của điểm M qua phép tịnh tiến theo véc tơ \(\overrightarrow{v}\)
là: \(\left\{{}\begin{matrix}x_C=2+1=3\\y_C=0+1=1\end{matrix}\right.\). Suy ra: \(C\left(3;1\right)\)
\(M''=Đ_{Oy}\left(C\right)\) nên \(\left\{{}\begin{matrix}x_{M''}=-x_C=-3\\y_{M''}=y_C=1\end{matrix}\right.\). Suy ra: \(M''\left(-3;1\right)\).