Lấy một mảnh giấy như trong Hình 1a, gọi một mép cắt là đoạn thẳng AB. Sau đó gấp mảnh giấy sao cho điểm A trùng với điểm B (Hình 1b)
Theo em nếp gấp xy có vuông góc với đoạn AB tại trung điểm hay không? Tại sao?
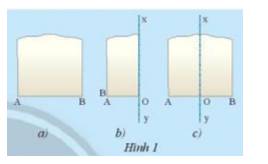
Lấy một mảnh giấy như trong Hình 1a, gọi một mép cắt là đoạn thẳng AB. Sau đó gấp mảnh giấy sao cho điểm A trùng với điểm B (Hình 1b)
Theo em nếp gấp xy có vuông góc với đoạn AB tại trung điểm hay không? Tại sao?

Cho hình chữ nhật ABCD, trên cạnh AB lấy các điểm M, N, P và trên cạnh DC lấy các điểm M’, N’, P’. Cho biết AM = MN = NP = PB và MM’, NN’, PP’ đều song song với BC (Hình 3). Tìm đường trung trực của mỗi đoạn thẳng AB, AN và NB.
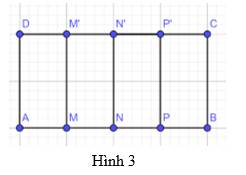
Đường trung trực của AB là NN’ vì NN' vuông góc với AB tại trung điểm N của AB.
Đường trung trực của AN là MM’ vì MM' vuông góc với AN tại trung điểm M của AN.
Đường trung trực của NB là PP’ vì PP' vuông góc với NB tại trung điểm P của NB.
Trả lời bởi Hà Quang MinhTrong Hình 4, hãy cho biết BD có là đường trung trực của đoạn thẳng AC hay không? Tại sao?
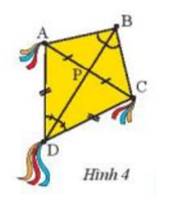
Theo giả thiết ta có P là trung điểm AC
Xét tam giác APD và tam giác CPD có :
AP = PC ( theo giả thiết )
DP cạnh chung
AD = CD ( theo giả thiết )
Suy ra t\(\Delta APD = \Delta CPD (c-c-c)\)
\( \Rightarrow \widehat {CPD} = \widehat {APD}\) (2 góc tương ứng )
Mà 2 góc ở vị trí kề bù \( \Rightarrow \widehat {CPD} = \widehat {APD} = {90^o}\)\( \Rightarrow AC \bot BD\) và P là chung điểm AC do AP = PC
\( \Rightarrow \) BD là đường trung trực của AC
Trả lời bởi Hà Quang MinhCho đoạn thẳng AB có O là trung điểm và d là đường trung trực. Lấy điểm M tùy ý thuộc d (Hình 5). Chứng minh rằng hai tam giác MOA và MOB bằng nhau, từ đó suy ra MA = MB
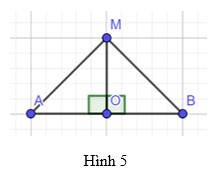
Theo giả thiết ta có O là trung điểm AB \( \Rightarrow \) AO = OB
Xét tam giác AOM và tam giác BOM có :
OM là cạnh chung
AO = OB
\(\widehat {MOA} = \widehat {MOB} = {90^o}\)(do d là trung trực AB)
(c-g-c)
\( \Rightarrow MA = MB\) (cạnh tương ứng)
Trả lời bởi Hà Quang MinhTrong Hình 8, cho biết d là đường trung trực của đoạn thẳng AB, điểm M thuộc đường thẳng d, MA = x + 2 và MB = 7. Tính x
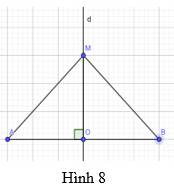
Vì M thuộc trung trực của AB \( \Rightarrow \) MA = MB \( \Rightarrow \) 7 = x + 2 \( \Rightarrow \) x = 5
Trả lời bởi Hà Quang MinhDựng đường trung trực của đoạn thẳng AB bằng thước thẳng và compa theo hướng dẫn sau:
- Lấy A làm tâm vẽ cung tròn bán kính lớn hơn \(\dfrac{1}{2}\)AB (Hình 9a)
- Lấy B làm tâm vẽ cung tròn có bán kính bằng bán kính ở trên (Hình 9b)
- Hai cung tròn này cắt nhau tại M và N (Hình 9c). Dùng thước vẽ đường thẳng MN. Hãy chứng minh đường thẳng MN chính là đường trung trực của đoạn thẳng AB.
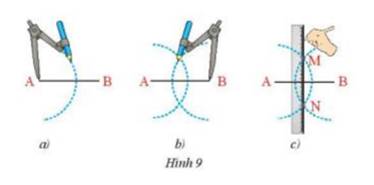
Vì 2 cung tròn cắt nhau tại M nên AM = MB = bán kính cung tròn
Chứng minh tương tự \( \Rightarrow \) AN = BN = bán kính cung tròn
\( \Rightarrow \) Vì M, N cách đều 2 đầu mút của đoạn AB nên M, N thuộc trung trực của AB
Và chỉ có 1 đường thẳng đi qua 2 điểm nên MN là trung trực của AB
Trả lời bởi Hà Quang MinhHình 10 minh họa một tờ giấy có hình vẽ đường trung trực xy của đoạn thẳng AB mà hình ảnh điểm B bị nhòe mất. Hãy nêu cách xác định điểm B.

Gọi giao điểm của AB và xy là O
\( \Rightarrow \) O là trung điểm AB (Do xy là đường trung trực của AB)
\( \Rightarrow \) Đo khoảng cách AO và từ điểm O kẻ OB sao cho OA = OB và nằm khác phía với điểm A so với đường thẳng xy (A, B, O thẳng hàng)
Trả lời bởi Hà Quang MinhQuan sát Hình 11, cho biết M là trung điểm của BC, AM vuông góc với BC và AB = 10 cm, Tính AC.
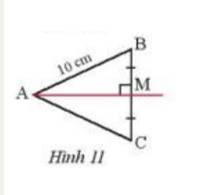
Xét tam giác AMB và tam giác AMC có :
AM cạnh chung
MB = MC (do M là trung điểm BC)
\(\widehat {BMA} = \widehat {CMA} = {90^o}\)
\( \Rightarrow \) Tam giác AMB = tam giác AMC (c-g-c)
\( \Rightarrow \)AB = AC = 10 cm ( cạnh tương ứng bằng nhau
Trả lời bởi Hà Quang MinhQuan sát Hình 12, cho biết AM là đường trung trực của đoạn thẳng BC và DB = DC = 8 cm. Chứng minh rằng ba điểm A, M, D thẳng hàng.
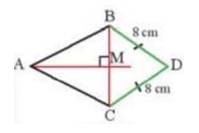
Xét tam giác BCD có BD = CD ( giả thiết )
\( \Rightarrow \) D thuộc trung trực BC do cách đều 2 đầu mút đoạn BC
Mà AM là trung trực của BC
\( \Rightarrow \) D thuộc đường thẳng AM
\( \Rightarrow \) A, M, D thẳng hàng
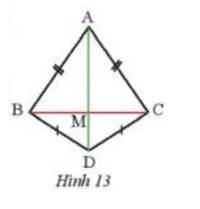
Trả lời bởi Hà Quang MinhQuan sát Hình 13, biết AB = AC, DB = DC. Chứng minh rằng M là trung điểm của BC.
Xét tam giác ABD và tam giác ACD có :
AB = AC ( giả thiết )
BD = CD ( giả thiết )
AD cạnh chung
\( \Rightarrow \Delta ABD =\Delta ACD (c-c-c)\)
\( \Rightarrow \)\(\widehat {BAD} = \widehat {CAD}\)( 2 góc tương ứng )
Xét tam giác ABM và ta giác ACM có :
AB = AC ( giả thiết )
AM cạnh chung
\(\widehat {BAD} = \widehat {CAD}\)( chứng minh trên )
\(\Delta ABM=\Delta ACM (c-g-c)\)
\(\Rightarrow MC = MB\) ( 2 cạnh tương ứng )
\( \Rightarrow \) M là trung điểm BC
Trả lời bởi Hà Quang Minh
Sau khi gấp A trùng với B thì điểm gấp trên cạnh AB là O
\( \Rightarrow \) AO = BO \( \Rightarrow \)O là trung điểm AB
Vì 2 mép của tờ giấy song song với nhau nên khi gấp đôi đường gấp ở giữa (xy) cũng song song với 2 cạnh của tờ giấy .
Mà 2 cạnh của tờ giấy vuông góc với AB nên xy cũng vuông góc với AB
Trả lời bởi Hà Quang Minh