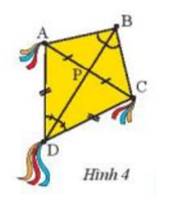
Theo giả thiết ta có P là trung điểm AC
Xét tam giác APD và tam giác CPD có :
AP = PC ( theo giả thiết )
DP cạnh chung
AD = CD ( theo giả thiết )
Suy ra t\(\Delta APD = \Delta CPD (c-c-c)\)
\( \Rightarrow \widehat {CPD} = \widehat {APD}\) (2 góc tương ứng )
Mà 2 góc ở vị trí kề bù \( \Rightarrow \widehat {CPD} = \widehat {APD} = {90^o}\)\( \Rightarrow AC \bot BD\) và P là chung điểm AC do AP = PC
\( \Rightarrow \) BD là đường trung trực của AC