Giải phương trình \(\frac{1}{{x - 1}} - \frac{{4x}}{{{x^3} - 1}} = \frac{x}{{{x^2} + x + 1}}.\)
Bài 4. Phương trình quy về phương trình bậc nhất một ẩn
HM
Hướng dẫn giải
Thảo luận (1)
HM
Giải các phương trình sau:
a) \(x\left( {x - 2} \right) = 0;\)
b) \(\left( {2x + 1} \right)\left( {3x - 2} \right) = 0.\)
Hướng dẫn giải
Thảo luận (1)
a) \(x\left( {x - 2} \right) = 0;\)
\(\begin{array}{l}TH1:x = 0\\TH2:x - 2 = 0\\x = 2\end{array}\)
Vậy \(x \in \left\{ {0;2} \right\}.\)
b) \(\left( {2x + 1} \right)\left( {3x - 2} \right) = 0.\)
\(\begin{array}{l}TH1:2x + 1 = 0\\x = \frac{{ - 1}}{2}\\TH2:3x - 2 = 0\\x = \frac{2}{3}\end{array}\)
Vậy \(x \in \left\{ {\frac{{ - 1}}{2};\frac{2}{3}} \right\}.\)
Trả lời bởi Hà Quang Minh
HM
Xét phương trình \(x + \frac{1}{{x + 1}} = - 1 + \frac{1}{{x + 1}}.\)
Chuyển các biểu thức chứa ẩn từ vế phải sang vế trái, rồi thu gọn vế trái.
Hướng dẫn giải
Thảo luận (1)
Ta có \(x + \frac{1}{{x + 1}} = - 1 + \frac{1}{{x + 1}}\) hay \(x + \frac{1}{{x + 1}} + 1 - \frac{1}{{x + 1}} = 0\) suy ra \(x + 1 = 0\)
Trả lời bởi Hà Quang Minh
HM
Xét phương trình \(\frac{{x + 3}}{x} = \frac{{x + 9}}{{x - 3}}.\left( 2 \right)\)
Hãy thực hiện các yêu cầu sau để giải phương trình (2):
a) Tìm điều kiện xác định của phương trình (2);
b) Quy đồng mẫu hai vế của phương trình (2), rồi khử mẫu;
c) Giải phương trình vừa tìm được;
d) Kết luận nghiệm của phương trình (2).
Hướng dẫn giải
Thảo luận (1)
a) ĐKXĐ \(x \ne 0\) và \(x \ne 3.\)
b) Quy đồng mẫu ta được \(\frac{{\left( {x + 3} \right)\left( {x - 3} \right)}}{{x\left( {x - 3} \right)}} = \frac{{\left( {x + 9} \right)x}}{{x\left( {x - 3} \right)}}\) và khử mẫu ta có: \(\left( {x - 3} \right)\left( {x + 3} \right) = x\left( {x + 9} \right)\)
c) \({x^2} - 9 = {x^2} + 9x\)
\(\begin{array}{l}{x^2} - {x^2} - 9x = 9\\ - 9x = 9\\x = - 1\end{array}\)
Giá trị \(x = - 1\left( {t/m} \right)\). Vậy nghiệm của phương trình là \(x = - 1.\)
Trả lời bởi Hà Quang Minh
HM
Xét phương trình \(x + \frac{1}{{x + 1}} = - 1 + \frac{1}{{x + 1}}.\)
Giá trị \(x = - 1\) có là nghiệm của phương trình đã cho hay không? Vì sao?
Hướng dẫn giải
Thảo luận (1)
Thay \(x = - 1\) vào phương trình đã cho ta có \(\left( { - 1} \right) + \frac{1}{{ - 1 + 1}} = - 1 + \frac{1}{{ - 1 + 1}}\), ta có kết quả đã cho chưa đúng vì khi thay \(x = - 1\) làm cho mẫu của phân số bằng 0.
Vậy \(x = - 1\) không là nghiệm của phương trình.
Trả lời bởi Hà Quang Minh
HM
Giải bài toán ở tình huống mở đầu.
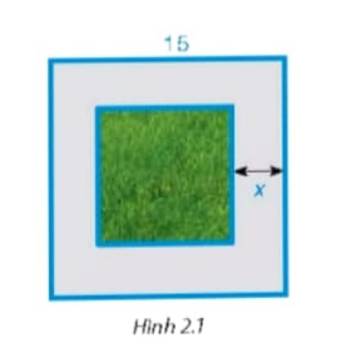
Tình huống mở đầu: Trong một khu vườn hình vuông có cạnh bằng 15m người ta làm một lối đi xung quanh vườn có bề rộng là x (m) (H.2.1). Để diện tích phần đất còn lại là \(169{m^2}\) thì bề rộng x của lối đi là bao nhiêu?
Hướng dẫn giải
Thảo luận (1)
Do lối đi có bề rộng là x nên cạnh của khu vườn hình vuông ban đầu giảm đi \(2x\left( m \right).\)
Nên phần đất còn lại là hình vuông có cạnh \(15 - 2x\left( m \right)\)
Diện tích phần đất còn lại là \(169{m^2}\) nên ta có phương trình \({\left( {15 - 2x} \right)^2} = 169\)
\(\begin{array}{l}{\left( {15 - 2x} \right)^2} = {13^2}\\TH1:15 - 2x = 13\\2x = 2\\x = 1\end{array}\)
\(TH2:15 - 2x = - 13\) (vô lý vì cạnh của mảnh đất >0)
Vậy \(x = 1\)
Vậy bề rộng của lối đi là 1m.
Trả lời bởi Hà Quang Minh
HM
Giải phương trình \(P\left( x \right) = 0.\)
Hướng dẫn giải
Thảo luận (1)
\(\begin{array}{l}P\left( x \right) = 0\\\left( {x + 1} \right)\left( {3x - 1} \right) = 0\\TH1:x + 1 = 0\\x = - 1\\TH2:3x - 1 = 0\\x = \frac{1}{3}\end{array}\)
Vậy \(x \in \left\{ { - 1;\frac{1}{3}} \right\}\)
Trả lời bởi Hà Quang Minh
HM
Phân tích đa thức \(P\left( x \right) = \left( {x + 1} \right)\left( {2x - 1} \right) + \left( {x + 1} \right)x\) thành nhân tử.
Hướng dẫn giải
Thảo luận (1)
\(P\left( x \right) = \left( {x + 1} \right)\left( {2x - 1} \right) + \left( {x + 1} \right)x = \left( {x + 1} \right)\left( {2x - 1 + x} \right) = \left( {x + 1} \right)\left( {3x - 1} \right)\)
Trả lời bởi Hà Quang Minh
HM
Giải các phương trình sau:
a) \(\left( {3x + 1} \right)\left( {2 - 4x} \right) = 0;\)
b) \({x^2} - 3x = 2x - 6.\)
Hướng dẫn giải
Thảo luận (1)
a) \(\left( {3x + 1} \right)\left( {2 - 4x} \right) = 0;\)
\(\begin{array}{l}TH1:3x + 1 = 0\\x = \frac{{ - 1}}{3}\\TH2:2 - 4x = 0\\x = \frac{1}{2}\end{array}\)
Vậy \(x \in \left\{ { - \frac{1}{3};\frac{1}{2}} \right\}\)
b) \({x^2} - 3x = 2x - 6.\)
\(\begin{array}{l}{x^2} - 3x = 2x + 6\\x\left( {x - 3} \right) = 2\left( {x + 3} \right)\\x\left( {x - 3} \right) - 2\left( {x + 3} \right) = 0\\\left( {x - 2} \right) - \left( {x - 3} \right) = 0\\TH1:x - 2 = 0\\x = 2\\TH2:x - 3 = 0\\x = 3\end{array}\)
Vậy \(x \in \left\{ {2;3} \right\}\)
Trả lời bởi Hà Quang Minh
HM
Tìm điều kiện xác định của mỗi phương trình sau:
a) \(\frac{{3x + 1}}{{2x - 1}} = 1;\)
b) \(\frac{x}{{x - 1}} + \frac{{x + 1}}{x} = 2.\)
Hướng dẫn giải
Thảo luận (1)
a) \(\frac{{3x + 1}}{{2x - 1}} = 1;\)
Vì \(2x - 1 \ne 0\) khi \(x \ne \frac{1}{2}.\) Vậy ĐKXĐ của phương trình đã cho là \(x \ne \frac{1}{2}.\)
b) \(\frac{x}{{x - 1}} + \frac{{x + 1}}{x} = 2.\)
Vì \(x - 1 \ne 0\) khi \(x \ne 1\) và \(x \ne 0\). Vậy ĐKXĐ của phương trình đã cho là \(x \ne 1\) và \(x \ne 0\).
Trả lời bởi Hà Quang Minh
ĐKXĐ: \(x \ne 1.\)
Quy đồng mẫu thức, ta được
\(\frac{{1.\left( {{x^2} + x + 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} - \frac{{4x}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} = \frac{{x\left( {x - 1} \right)}}{{\left( {{x^2} + x + 1} \right)\left( {x - 1} \right)}}\)
Khử mẫu ta được \({x^2} + x + 1 - 4x = x\left( {x - 1} \right)\)
\(\begin{array}{l}{x^2} + x + 1 - 4x = {x^2} - x\\{x^2} - 3x - {x^2} + x = - 1\\ - 2x = - 1\end{array}\)
\(x = \frac{1}{2}\left( {t/m} \right).\)
Vậy nghiệm của phương trình là \(x = \frac{1}{2}.\)
Trả lời bởi Hà Quang Minh