Cho hàm số \(y = {x^2} - 4x + 3\). Thực hiện lần lượt các yêu cầu sau:
a) Tính y’ và tìm các điểm tại đó \(y' = 0\).
b) Xét dấu y’ để tìm các khoảng đồng biến, khoảng nghịch biến và cực trị của hàm số.
c) Tính \(\mathop {\lim }\limits_{x \to - \infty } y\), \(\mathop {\lim }\limits_{x \to + \infty } y\) và lập bảng biến thiên của hàm số.
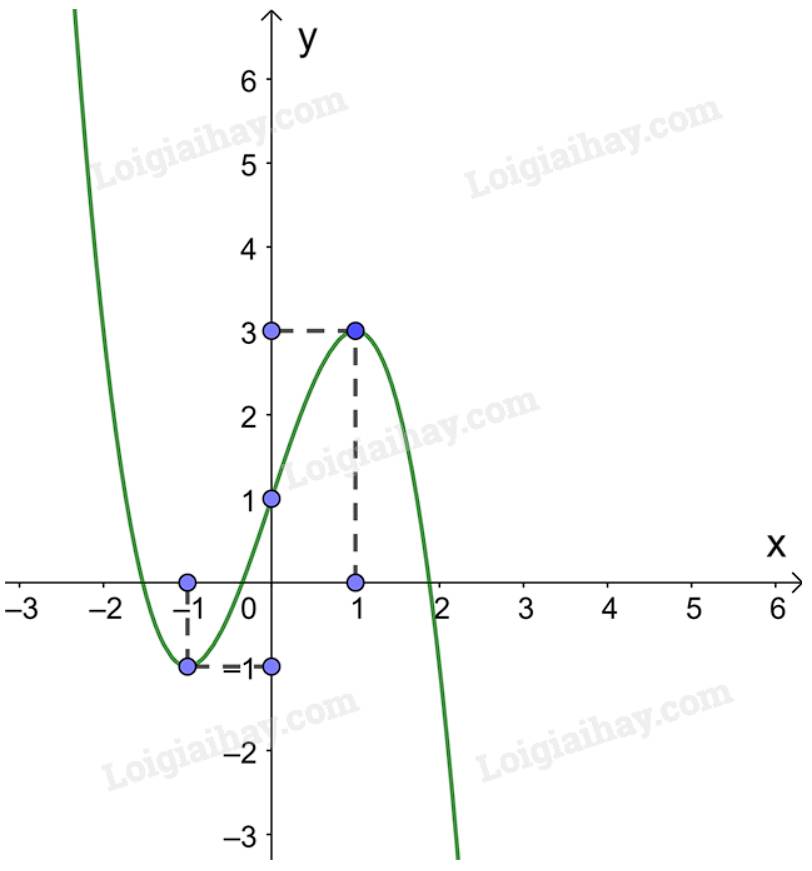
d) Vẽ đồ thị của hàm số và nhận xét về tính đối xứng của đồ thị.

a) Tập xác định: \(D = \mathbb{R}\)
Ta có: \(y' = 2x - 4,y' = 0 \Leftrightarrow 2x - 4 = 0 \Leftrightarrow x = 2\)
Vậy với \(x = 2\) thì \(y' = 0\).
b) Trên khoảng \(\left( { - \infty ;2} \right)\), \(y' < 0\) nên hàm số nghịch biến. Trên khoảng \(\left( {2; + \infty } \right)\), \(y' > 0\) nên hàm số đồng biến.
Hàm số đạt cực tiểu tại \(x = 2,\) giá trị cực tiểu \({y_{CT}} = - 1\). Hàm số không có cực đại.
c) \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {{x^2} - 4x + 3} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {{x^2}\left( {1 - \frac{4}{x} + \frac{3}{{{x^2}}}} \right)} \right] = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( {{x^2} - 4x + 3} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ {{x^2}\left( {1 - \frac{4}{x} + \frac{3}{{{x^2}}}} \right)} \right] = + \infty \)
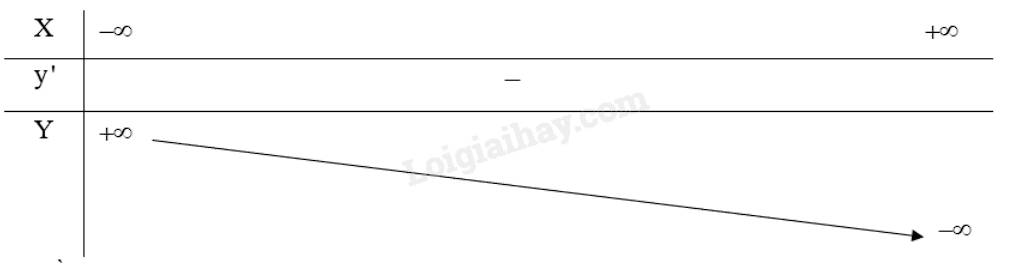
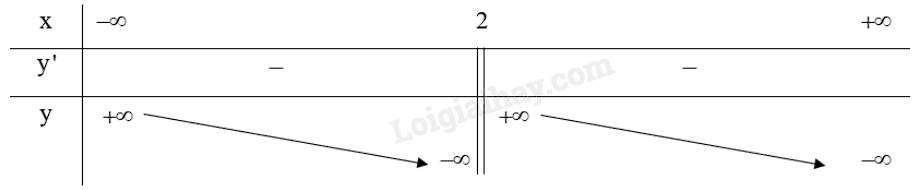
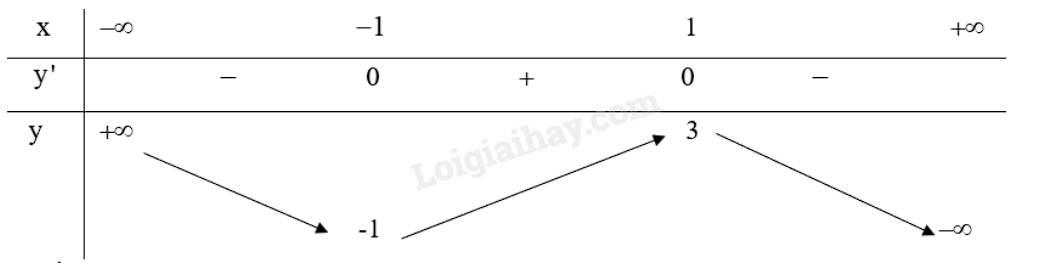
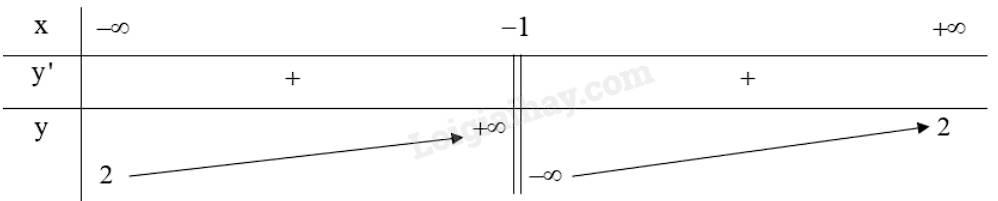
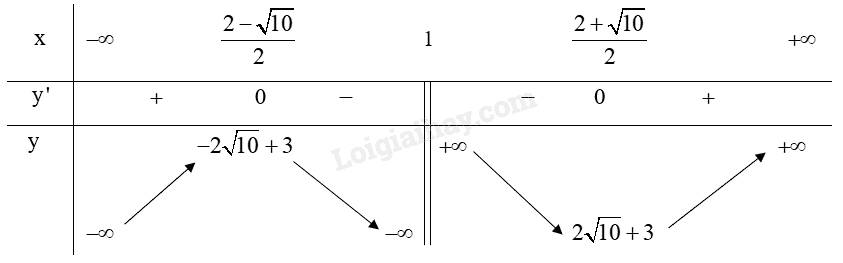
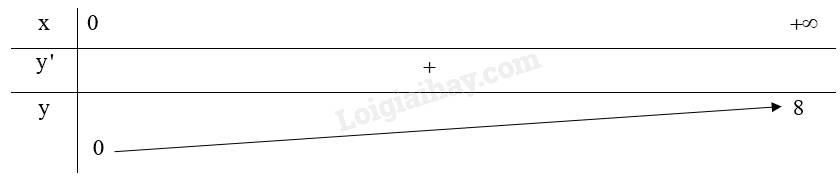
Bảng biến thiên:
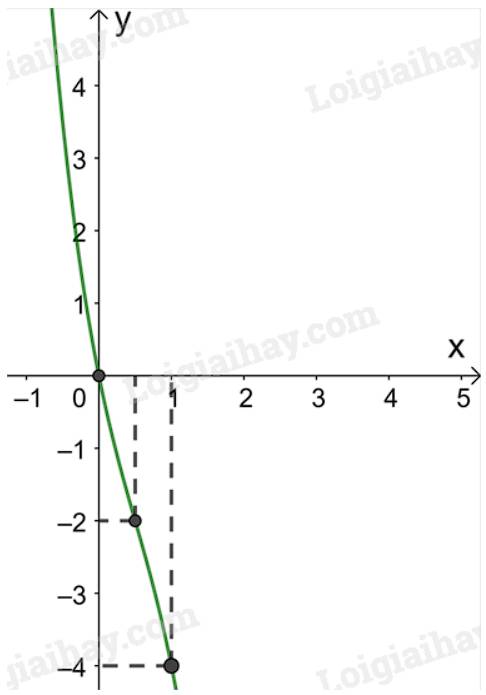
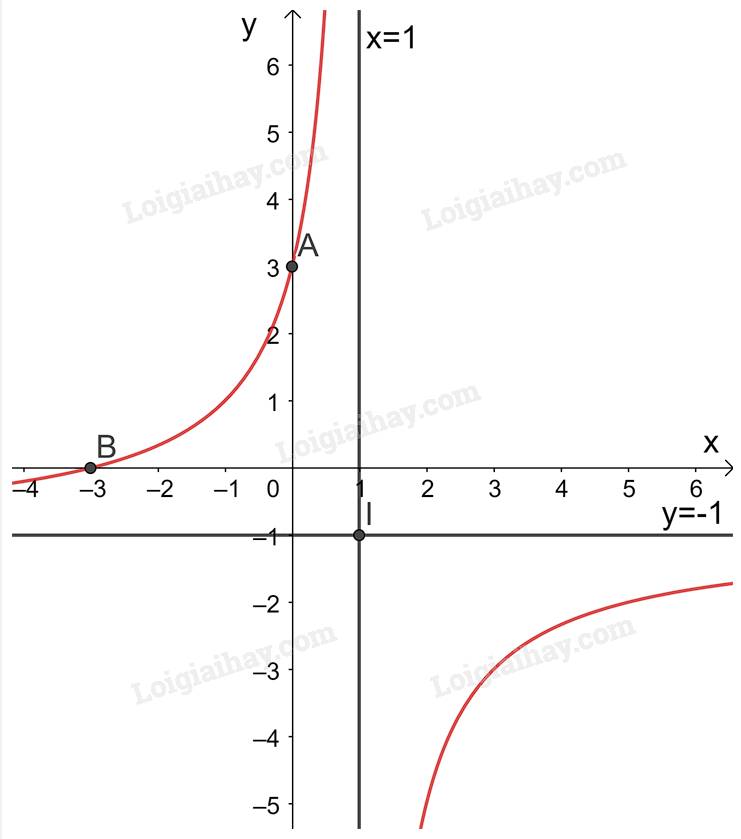
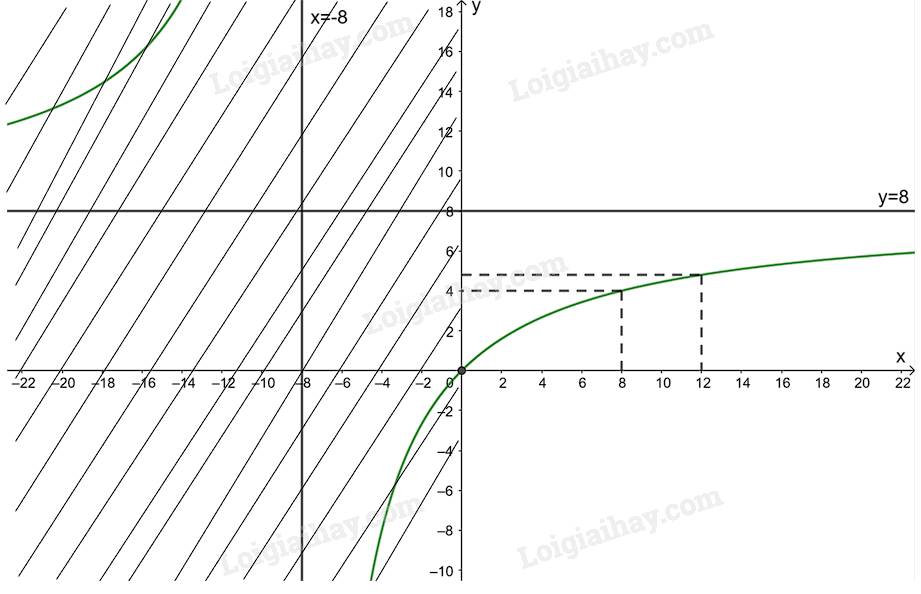
d) Giao điểm của đồ thị hàm số \(y = {x^2} - 4x + 3\) với trục tung là \(\left( {0;3} \right)\).
Ta có: \({x^2} - 4x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\). Do đó, giao điểm của đồ thị hàm số với trục hoành là các điểm \(\left( {3;0} \right);\left( {1;0} \right)\).
Điểm \(\left( {4;3} \right)\) thuộc đồ thị hàm số \(y = {x^2} - 4x + 3\).
Đồ thị hàm số nhận đường thẳng \(x = 2\) làm trục đối xứng.
Trả lời bởi Hà Quang Minh