Giải bài toán ở tình huống mở đầu, coi f(x) là hàm số xác định với \(x \ge 1\).
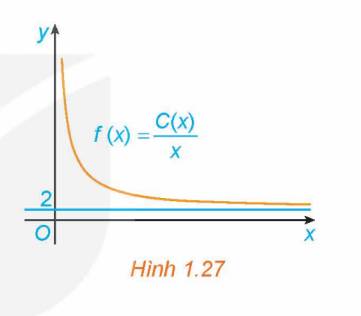
Một đơn vị sản xuất hàng tiêu dùng ước tính chi phí để sản xuất x đơn vị sản phẩm là \(C\left( x \right) = 2x + 45\) (triệu đồng). Khi đó, chi phí trung bình cho mỗi đơn vị sản phẩm là \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\). Hãy giải thích tại sao chi phí trung bình giảm theo x nhưng luôn lớn hơn 2 triệu đồng/ sản phẩm. Điều này thể hiện trên đồ thị của hàm số f(x) trong Hình 1.27 như thế nào?
Ta có: \(f\left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{2x + 45}}{x}\)
Vì \(f'\left( x \right) = \frac{{ - 45}}{{{x^2}}} < 0\) với mọi \(x \ge 1\) nên hàm số \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\) là hàm số giảm.
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 45}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 + \frac{{45}}{x}}}{1} = 2\)
Do đó, chi phí trung bình giảm theo x nhưng luôn lớn 2 triệu đồng/ sản phẩm.
Điều này được thể hiện trong Hình 1.27 là đồ thị hàm số \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\) có tiệm cận ngang là đường thẳng \(y = 2\) và đi xuống trong khoảng \(\left( {0; + \infty } \right)\).
