Cho hai điểm A(1; 0; 0) và B(5; 0; 0). Chứng minh rằng nếu điểm M(x; y; z) thỏa mãn \(\overrightarrow{MA}.\overrightarrow{MB}=0\) thì M thuộc một mặt cầu (S). Tìm tâm và bán kính của (S).
Bài 3: Phương trình mặt cầu
H24
Hướng dẫn giải
Thảo luận (1)
H24
Phần mềm mô phỏng thiết bị thám hiểm đại dương có dạng hình cầu trong không gian Oxyz. Cho biết tọa độ tâm mặt cầu là I(360; 200; 400) và bán kính r = 2 m. Viết phương trình mặt cầu.

Hướng dẫn giải
Thảo luận (1)
Phương trình mặt cầu tâm \(I\left( {360;200;400} \right)\), bán kính \(R = 2\) là
\({\left( {x - 360} \right)^2} + {\left( {y - 200} \right)^2} + {\left( {z - 400} \right)^2} = 4\)
Trả lời bởi datcoder
H24
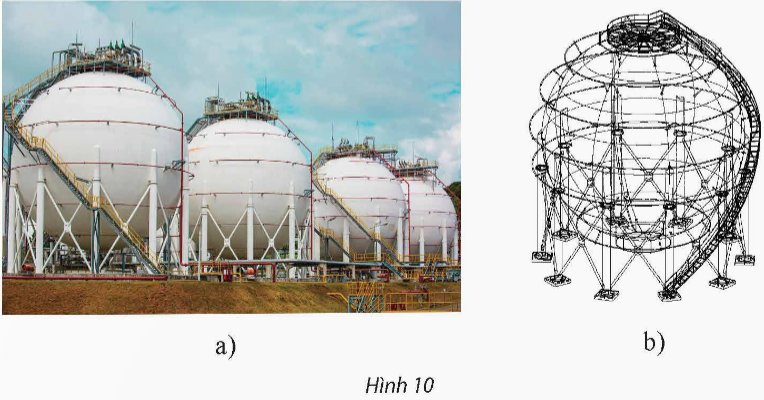
Người ta muốn thiết kế một bồn chứa khí hóa lỏng hình cầu bằng phần mềm 3D. Cho biết phương trình bề mặt của bồn chứa là (S): (x – 6)2 + (y – 6)2 + (z – 6)2 25. Phương trình mặt phẳng chứa nắp là (P): z 10.a) Tìm tâm và bán kính của bồn chứa.b) Tính khoảng cách từ tâm bồn chứa đến mặt phẳng chứa nắp.
Đọc tiếp
Người ta muốn thiết kế một bồn chứa khí hóa lỏng hình cầu bằng phần mềm 3D. Cho biết phương trình bề mặt của bồn chứa là (S): (x – 6)2 + (y – 6)2 + (z – 6)2 = 25. Phương trình mặt phẳng chứa nắp là (P): z = 10.
a) Tìm tâm và bán kính của bồn chứa.
b) Tính khoảng cách từ tâm bồn chứa đến mặt phẳng chứa nắp.
Hướng dẫn giải
Thảo luận (1)
a) Phương trình bề mặt bồn chứa là \(\left( S \right):{\left( {x - 6} \right)^2} + {\left( {y - 6} \right)^2} + {\left( {z - 6} \right)^2} = 25\), nên bồn chứa là một hình cầu có tâm \(I\left( {6;6;6} \right)\) và bán kính \(R = \sqrt {25} = 5\).
b) Khoảng cách từ tâm bồn chứa \(I\left( {6;6;6} \right)\) đến mặt phẳng chứa nắp \(\left( P \right):z - 10 = 0\) là \(d = \frac{{\left| {0.6 + 0.6 + 1.6 - 10} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = 4\).
Trả lời bởi datcoder
Ta có \(\overrightarrow {MA} = \left( {1 - x;y;z} \right)\) và \(\overrightarrow {MB} = \left( {5 - x;y;z} \right)\).
Do \(\overrightarrow {MA} .\overrightarrow {MB} = 0\) nên
\(\begin{array}{l}\left( {1 - x} \right)\left( {5 - x} \right) + {y^2} + {z^2} = 0\\ \Rightarrow {x^2} - 6x + 5 + {y^2} + {z^2} = 0\\ \Rightarrow \left( {{x^2} - 6x + 9} \right) + {y^2} + {z^2} = 4\\ \Rightarrow {\left( {x - 3} \right)^2} + {y^2} + {z^2} = 4\end{array}\)
Vậy điểm \(M\left( {x;y;z} \right)\) thuộc mặt cầu \(S\) có tâm \(I\left( {3;0;0} \right)\) và bán kính \(R = \sqrt 4 = 2\).
Trả lời bởi datcoder