Quan sát Hình 32 và cho biết:
a) Hình chiếu của đường thẳng \(MO\) trên mặt phẳng \(\left( P \right)\) là đường thẳng nào;
b) Góc giữa đường thẳng \(MO\) và hình chiếu của đường thẳng đó trên mặt phẳng \(\left( P \right)\) là góc nào.
Quan sát Hình 32 và cho biết:
a) Hình chiếu của đường thẳng \(MO\) trên mặt phẳng \(\left( P \right)\) là đường thẳng nào;
b) Góc giữa đường thẳng \(MO\) và hình chiếu của đường thẳng đó trên mặt phẳng \(\left( P \right)\) là góc nào.
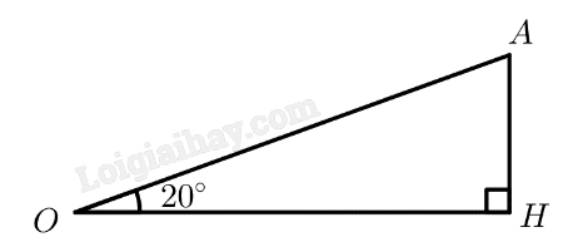
Giả sử ở những giây đầu tiên sau khi cất cánh. máy bay chuyển động theo một đường thẳng tạo với mặt đất một góc \({20^ \circ }\) và có vận tốc 200 km/h. Tính độ cao của máy bay so với mặt đất theo đơn vị mét sau khi máy bay rời khỏi mặt đất 2 giây (làm tròn kết quả đến hàng phần mười).
Đổi \(200km/h = \frac{{500}}{9}m/s\)
Mô hình hoá như hình vẽ, với \(OA\) là quãng đường máy bay bay được sau 2 giây, \(OH\) là độ cao của máy bay so với mặt đấy khi máy bay bay được sau 2 giây, độ lớn của góc \(\widehat {AOH}\) chỉ số đo góc giữa máy bay với mặt đất.
Sau 2 giây máy bay bay được quãng đường là: \(\frac{{500}}{9}.2 = \frac{{1000}}{9}\left( m \right)\)
Vì tam giác \(OAH\) vuông tại \(H\) nên ta có:
\(AH = OA.\sin \widehat {AOH} = \frac{{1000}}{9}.\sin {20^ \circ } \approx 38,0\left( m \right)\)
Vậy độ cao của máy bay so với mặt đất là 38 mét sau khi máy bay rời khỏi mặt đất 2 giây.
Trả lời bởi Quoc Tran Anh LeCho góc nhị diện có hai mặt là hai nửa mặt phẳng \(\left( P \right),\left( Q \right)\) và cạnh của góc nhị diện là đường thẳng \(d\).
Qua một điểm \(O\) trên đường thẳng \(d\), ta kẻ hai tia \(Ox,Oy\) lần lượt thuộc hai nửa mặt phẳng \(\left( P \right),\left( Q \right)\) và cùng vuông góc với đường thẳng \(d\). Góc \(xOy\) gọi là góc phẳng nhị diện của góc nhị diện đã cho (Hình 38).
Giả sử góc \(x'Oy'\) cũng là góc phẳng nhị diện của góc nhị diện đã cho với \(O'\) khác \(O\) (Hình 39).
Hãy so sánh số đo của hai góc \(xOy\) và \(x'Oy'\).
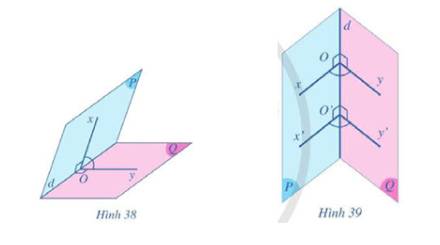
Trong \(\left( P \right)\) ta có:
\(\left. \begin{array}{l}Ox \bot d\\O'x' \bot d\end{array} \right\} \Rightarrow Ox\parallel O'x'\)
Trong \(\left( Q \right)\) ta có:
\(\left. \begin{array}{l}Oy \bot d\\O'y' \bot d\end{array} \right\} \Rightarrow Oy\parallel O'y'\)
Vậy \(\left( {Ox,Oy} \right) = \left( {O'x',O'y'} \right)\) hay số đo của hai góc \(xOy\) và \(x'Oy'\) bằng nhau.
Trả lời bởi Quoc Tran Anh LeCho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông và \(SA \bot \left( {ABCD} \right)\). Tính số đo theo đơn vị độ của góc nhị diện:
a) \(\left[ {B,SA,D} \right]\);
b) \(\left[ {B,SA,C} \right]\).
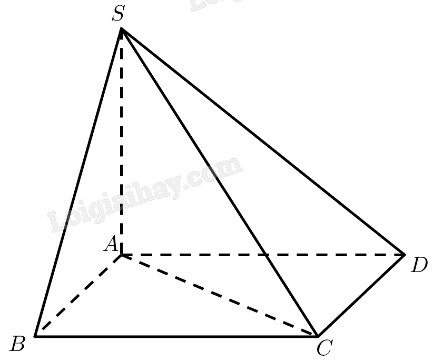
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{D}}\)
Vậy \(\widehat {BA{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,D} \right]\)
\(ABCD\) là hình vuông \( \Rightarrow \widehat {BA{\rm{D}}} = {90^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,D} \right]\) bằng \({90^ \circ }\).
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{C}}\)
Vậy \(\widehat {BA{\rm{C}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,C} \right]\)
\(ABCD\) là hình vuông \( \Rightarrow \widehat {BA{\rm{C}}} = {45^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,C} \right]\) bằng \({45^ \circ }\).
Trả lời bởi Quoc Tran Anh Le\(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình thoi cạnh \(a\) và \(AC = a\).
a) Tính số đo của góc nhị diện \(\left[ {B,SA,C} \right]\).
b) Tính số đo của góc nhị diện \(\left[ {B,SA,D} \right]\).
c) Biết \(SA = a\), tính số đo của góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABCD} \right)\).
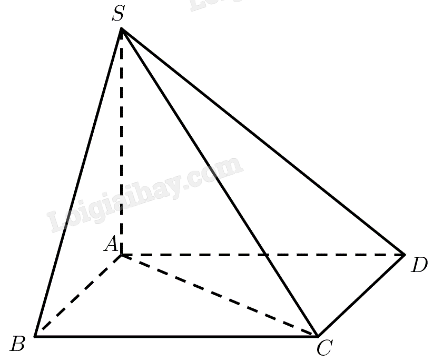
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{C}}\)
Vậy \(\widehat {BA{\rm{C}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,C} \right]\)
\(AB = BC = AC = a \Rightarrow \Delta ABC\) đều \( \Rightarrow \widehat {BA{\rm{C}}} = \widehat {ABC} = {60^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,C} \right]\) bằng \({60^ \circ }\).
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{D}}\)
Vậy \(\widehat {BA{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,D} \right]\)
\(ABCD\) là hình thoi \( \Rightarrow \widehat {BA{\rm{D}}} = {180^ \circ } - \widehat {ABC} = {180^ \circ } - {60^ \circ } = {120^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,D} \right]\) bằng \({120^ \circ }\).
c) \(SA \bot \left( {ABCD} \right) \Rightarrow \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
\(\Delta SAC\) vuông tại \(A \Rightarrow \tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{a}{a} = 1 \Rightarrow \widehat {SCA} = {45^ \circ }\)
Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = {45^ \circ }\).
Trả lời bởi Quoc Tran Anh LeCho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, hai đường thẳng \(AC\) và \(BD\) cắt nhau tại \(O\), \(SO \bot \left( {ABCD} \right)\), tam giác \(SAC\) là tam giác đều.
a) Tính số đo của góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABCD} \right)\).
b) Chứng minh rằng \(AC \bot \left( {SBD} \right)\). Tính số đo của góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {SBD} \right)\).
c) Gọi \(M\) là trung điểm của cạnh \(AB\). Tính số đo của góc nhị diện \(\left[ {M,SO,D} \right]\).
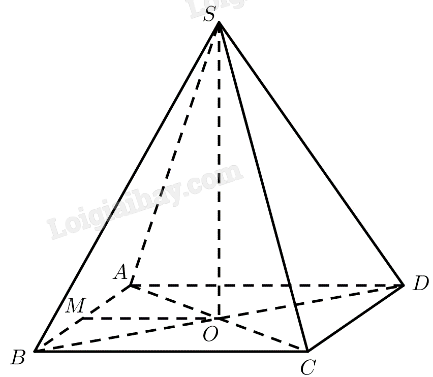
a) \(SO \bot \left( {ABCD} \right) \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = \left( {SA,OA} \right) = \widehat {SAO}\)
Tam giác \(SAC\) là tam giác đều \( \Rightarrow \widehat {SAO} = {60^ \circ }\)
\( \Rightarrow \left( {SA,\left( {ABCD} \right)} \right) = {60^ \circ }\)
b) \(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC\)
\( \Rightarrow AC \bot \left( {SB{\rm{D}}} \right)\)
\( \Rightarrow \left( {SA,\left( {SB{\rm{D}}} \right)} \right) = \left( {SA,SO} \right) = \widehat {ASO} = \frac{1}{2}\widehat {ASC} = {30^ \circ }\)
c) \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot MO,SO \bot DO\)
Vậy \(\widehat {MO{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {M,SO,D} \right]\)
\(ABCD\) là hình vuông \(\widehat {AOD} = {90^ \circ }\)
\(\Delta AMO\) vuông cân tại \(M \Rightarrow \widehat {AOM} = {45^ \circ }\)
\( \Rightarrow \widehat {MO{\rm{D}}} = \widehat {AOM} + \widehat {AO{\rm{D}}} = {45^ \circ } + {90^ \circ } = {135^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {M,SO,D} \right]\) bằng \({135^ \circ }\).
Trả lời bởi Quoc Tran Anh LeDốc là đoạn đường thẳng nối hai khu vực hay hai vùng có độ cao khác nhau. Độ dốc được xác định bằng góc giữa dốc và mặt phẳng nằm ngang, ở đó độ dốc lớn nhất là 100%, tương ứng với góc \({90^ \circ }\) (độ dốc 10% tương ứng với góc \({9^ \circ }\)). Giả sử có hai điểm \(A,B\) nằm ở độ cao lần lượt là 200 m, 220 m so với mực nước biển và đoạn dốc \(AB\) dài 120 m. Độ dốc đó bằng bao nhiêu phần trăm (làm tròn kết quả đến hàng phần trăm?
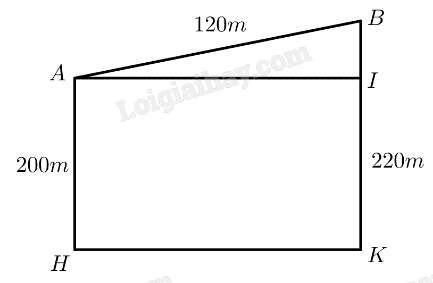
Mô hình hoá như hình vẽ, với \(AB\) là chiều dài con dốc, \(AH\) là độ cao của điểm \(A\) so với mặt nước biển, \(BK\) là độ cao của điểm \(B\) so với mặt nước biển, \(BI\) là chiều cao của con dốc, độ lớn của góc \(\widehat {BAI}\) chỉ độ dốc.
Ta có: \(AH = 200,BK = 220,AB = 120\).
\(AHKB\) là hình chữ nhật \( \Rightarrow IK = AH = 200 \Rightarrow BI = BK - IK = 220 - 200 = 20\)
Vì tam giác \(ABI\) vuông tại \(I\) nên ta có:
\(\sin \widehat {ABI} = \frac{{BI}}{{AB}} = \frac{{20}}{{120}} = \frac{1}{6} \Rightarrow \widehat {ABI} \approx 9,{59^ \circ }\) tương ứng với 10,66%
Vậy độ dốc của con dốc đó là 10,66%.
Trả lời bởi Quoc Tran Anh LeTrong Hình 42, máy tính xách tay đang mở gợi nên hình ảnh của một góc nhị diện. Ta gọi số đo góc nhị diện đó là độ mở của màn hình máy tính. Tính độ mở của màn hình máy tính theo đơn vị độ, biết tam giác \(ABC\) có độ dài các cạnh là \(AB = AC = 30{\rm{ }}cm\) và \(BC = 30\sqrt 3 {\rm{ }}cm\).

Cách 1:
\(\dfrac{BC}{sin\widehat{A}}=\dfrac{AB}{sin\widehat{C}}=\dfrac{AC}{sin\widehat{B}}\)
Ta có \(\widehat{C}=\widehat{B}\) ( tam giác ABC cân tại A )
\(\widehat{B}+\widehat{C}=180^0-\widehat{A}\) \(\Leftrightarrow2\widehat{B}=180^0-\widehat{A}\Leftrightarrow\widehat{B}=90^0-\dfrac{\widehat{A}}{2}\)
\(\Rightarrow sin\widehat{B}=sin\left(90^0-\dfrac{\widehat{A}}{2}\right)=cos\left(\dfrac{\widehat{A}}{2}\right)\)
\(\Rightarrow\dfrac{BC}{sin\widehat{A}}=\dfrac{AC}{cos\left(\dfrac{\widehat{A}}{2}\right)}\) \(\Leftrightarrow\sqrt{3}.cos\left(\dfrac{\widehat{A}}{2}\right)=2.sin\left(\dfrac{\widehat{A}}{2}\right).cos\left(\dfrac{\widehat{A}}{2}\right)\)
( tam giác ABC có \(\widehat{A}\ne180^0\Rightarrow\dfrac{\widehat{A}}{2}\ne90^0\Rightarrow cos\left(\dfrac{\widehat{A}}{2}\right)\ne0\) )
\(\Rightarrow\sqrt{3}=2sin\left(\dfrac{\widehat{A}}{2}\right)\) \(\Leftrightarrow\dfrac{\widehat{A}}{2}=60^0\Leftrightarrow\widehat{A}=120^0\)
Vậy độ mở của màn hình máy tính là \(120^0\)
Cách 2: Do AB=AC nên tam giác ABC cân tại A
Kẻ \(AH\perp BC\) tại H
Tam giác ABC cân tại A có AH vừa là đường cao, vừa là đường phân giác, vừa là đường trung tuyến
\(\Rightarrow\)H là trung điểm của BC \(\Rightarrow BH=\dfrac{BC}{2}=15\sqrt{3}\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông có:
\(sin\widehat{BAH}=\dfrac{BH}{AB}=\dfrac{\sqrt{3}}{2}\Rightarrow\widehat{BAH}=60^0\)
\(\Rightarrow\widehat{BAC}=2\widehat{BAH}=120^0\)
Vậy độ mở của màn hình máy tính là \(120^0\)
Trả lời bởi GấuuTrong Hình 43, xét các góc nhị diện có góc phẳng nhị diện tương ứng là \(\widehat B,\widehat C,\widehat D,\widehat E\) trong cùng mặt phẳng. Lục giác \(ABCDEG\) nằm trong mặt phẳng đó có \(AB = GE = 2{\rm{ }}m,BC = DE,\widehat A = \widehat G = {90^ \circ },\widehat B = \widehat E = x,\widehat C = \widehat D = y\). Biết rằng khoảng cách từ \(C\) và \({\rm{D}}\) đến \({\rm{AG}}\) là \(4{\rm{ }}m\), \(AG = 12{\rm{ }}m,CD = 1{\rm{ }}m\). Tìm x, y (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).

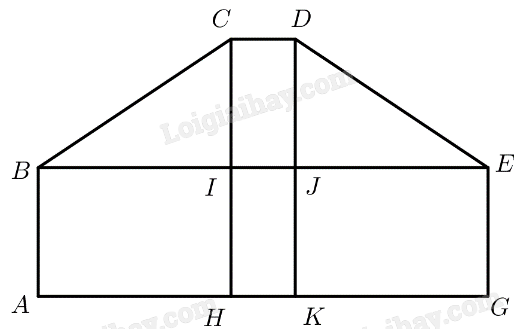
Kẻ \(CH \bot AG\left( {H \in AG} \right),DK \bot AG\left( {K \in AG} \right)\)
Gọi \(I = BE \cap CH,J = BE \cap DK\).
\(ABEG\) là hình chữ nhật \( \Rightarrow BE = AB = 12\)
\(C{\rm{D}}KH,C{\rm{D}}JI\) là hình chữ nhật \( \Rightarrow HK = IJ = C{\rm{D}} = 1\)
\(ABIH,EGKJ\) là hình chữ nhật \( \Rightarrow IH = JK = AB = 2\)
\(AH = GK = BI = EJ = \frac{{AG - HK}}{2} = \frac{{12 - 1}}{2} = 5,5\)
\(CH = d\left( {C,AG} \right) = 4 \Rightarrow CI = CH - IH = 4 - 2 = 2\)
\(\Delta BCI\) vuông tại \(I\)\( \Rightarrow \tan \widehat {CBI} = \frac{{CI}}{{BI}} = \frac{2}{{5,5}} = \frac{4}{{11}} \Rightarrow \widehat {CBI} \approx 19,{98^ \circ }\)
\(\begin{array}{l} \Rightarrow x = \widehat {ABI} + \widehat {CBI} = {90^ \circ } + 19,{98^ \circ } = 110,{0^ \circ }\\ \Rightarrow y = {180^ \circ } - x = {180^ \circ } - 110,{0^ \circ } = 70,{0^ \circ }\end{array}\)
Trả lời bởi Quoc Tran Anh LeCho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\). Gọi \(\alpha \) là số đo của góc nhị diện \(\left[ {A,BC,S} \right]\). Chứng minh rằng tỉ số diện tích của hai tam giác \(ABC\) và \(SBC\) bằng \(\cos \alpha \).
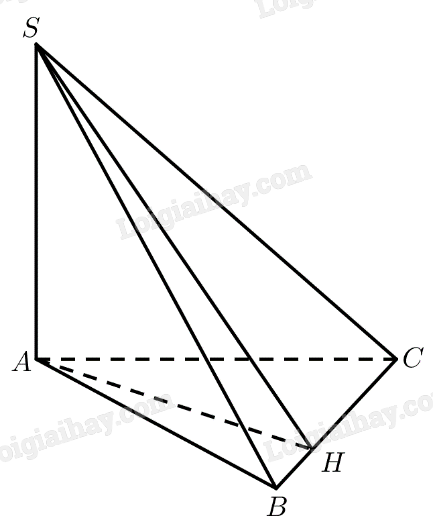
Kẻ \(AH \bot BC\left( {H \in BC} \right)\)
\(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\)
\( \Rightarrow BC \bot \left( {SAH} \right) \Rightarrow BC \bot SH\)
Vậy \(\widehat {SHA}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,BC,S} \right]\)
\( \Rightarrow \widehat {SHA} = \alpha \)
\(\begin{array}{l}{S_{\Delta ABC}} = \frac{1}{2}BC.AH,{S_{\Delta SBC}} = \frac{1}{2}BC.SH\\ \Rightarrow \frac{{{S_{\Delta ABC}}}}{{{S_{\Delta SBC}}}} = \frac{{\frac{1}{2}BC.AH}}{{\frac{1}{2}BC.SH}} = \frac{{AH}}{{SH}} = \cos \widehat {SHA} = \cos \alpha \end{array}\)
Trả lời bởi Quoc Tran Anh Le
a) Vì \(MH \bot \left( P \right),O \in \left( P \right)\) nên hình chiếu của đường thẳng \(MO\) trên mặt phẳng \(\left( P \right)\) là đường thẳng \(HO\)
b) Góc giữa đường thẳng \(MO\) và hình chiếu của đường thẳng đó trên mặt phẳng \(\left( P \right)\) là góc \(\widehat {MOH}\).
Trả lời bởi Quoc Tran Anh Le