Liệu phân thức nào đơn giản nhưng bằng phân thức \(\frac{{x - y}}{{{x^3} - {y^3}}}\) không nhỉ?
Bài 22. Tính chất cơ bản của phân thức đại số
QL
Hướng dẫn giải
Thảo luận (1)
QL
Nếu nhân cả tử và mẫu của phân thức \(\frac{{x + y}}{{x - y}}\) với 2x ta được phân thức mới nào? Giải thích vì sao phân thức mới nhận được bằng phân thức đã cho.
Hướng dẫn giải
Thảo luận (1)
Nhân cả tử và mẫu của phân thức \(\frac{{x + y}}{{x - y}}\) với 2x, ta có: \(\frac{{2{\rm{x}}\left( {x + y} \right)}}{{2{\rm{x}}\left( {x - y} \right)}}\)
Phân thức mới nhận được bằng phân thức đã cho vì cả tử và mẫu của phân thức đều nhân cùng với một số.
Trả lời bởi Hà Quang Minh
QL
Tử và mẫu của phân thức \(\frac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)có nhân tử chung là x−1. Viết phân thức nhận được sau khi chia cả tử và mẫu của phân thức này cho nhân tử chung đó. So sánh phân thức mới nhận được với phân thức đã cho.
Hướng dẫn giải
Thảo luận (1)
Chia cả tử và mẫu của phân thức này cho nhân tử chung x−1, ta có \(\frac{{x + 1}}{{{x^2} + x + 1}}\)
=> Phân thức mới được rút gọn và mất đi nhân tử chung x−1
Trả lời bởi Hà Quang Minh
QL
Khẳng định sau đúng hay sai? Vì sao?
\(\frac{{30{\rm{x}}{y^2}\left( {x - y} \right)}}{{45{\rm{x}}y{{\left( {x - y} \right)}^2}}} = \frac{{2y}}{{3\left( {x - y} \right)}}\)
Hướng dẫn giải
Thảo luận (2)
Khẳng định trên là đúng. Vì nhân cả tử và mẫu của phân thức \(\frac{{2y}}{{3\left( {x - y} \right)}}\) với 15 ta được phân thức
\(\frac{{30{\rm{x}}{y^2}\left( {x - y} \right)}}{{45{\rm{x}}y{{\left( {x - y} \right)}^2}}} \Rightarrow \frac{{30{\rm{x}}{y^2}\left( {x - y} \right)}}{{45{\rm{x}}y{{\left( {x - y} \right)}^2}}} = \frac{{2y}}{{3\left( {x - y} \right)}}\)
Trả lời bởi Hà Quang Minh
QL
Giải thích vì sao \(\frac{{ - x}}{{1 - x}} = \frac{x}{{x - 1}}\)
Hướng dẫn giải
Thảo luận (1)
Nhân cả tử và mẫu của phân thức \(\frac{x}{{x - 1}}\) với -1 ta được phân thức \(\frac{{ - x}}{{1 - x}} \Rightarrow \frac{{ - x}}{{1 - x}} = \frac{x}{{x - 1}}\)
Trả lời bởi Hà Quang Minh
QL
Phân tích tử và mẫu của phân thức \(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}}\) thành nhân tử và tìm các nhân tử chung của chúng
Hướng dẫn giải
Thảo luận (1)
Ta có: \(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}} = \frac{{2{\rm{x}}\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}}\)
Nhân tử chung là x + 1
Trả lời bởi Hà Quang Minh
QL
Chia cả tử và mẫu của phân thức \(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}}\) cho các nhân tử chung, ta nhận được một phân thức mới bằng phân thức đã cho nhưng đơn giản hơn
Hướng dẫn giải
Thảo luận (1)
Ta có: \(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}} = \frac{{2{\rm{x}}\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x - 1} \right)}} = \frac{{2{\rm{x}}}}{{x + 1}}\)
Trả lời bởi Hà Quang Minh
QL
Liệu phân thức nào đơn giản nhưng bằng phân thức \(\frac{{x - y}}{{{x^3} - {y^3}}}\) không nhỉ?
Hướng dẫn giải
Thảo luận (1)
Ta có: \(\frac{{x - y}}{{{x^3} - {y^3}}} = \frac{{x - y}}{{\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)}} = \frac{1}{{{x^2} + xy + {y^2}}}\)
Trả lời bởi Hà Quang Minh
QL
Thực hiện rút gọn một phân thức như hình bên. Hỏi bạn tròn làm đúng hay sai? Vì sao?
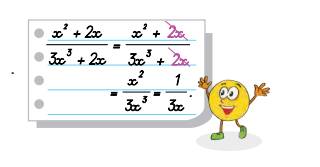
Hướng dẫn giải
Thảo luận (1)
Bạn tròn làm thế là sai. Vì bạn bỏ hai số hạng giống nhau của cả tử và mẫu là 2x chứ không phải chia cho nhân tử chung của cả tử và mẫu.
Trả lời bởi Hà Quang Minh
QL
Tìm a sao cho hai phân thức sau bằng nhau: \(\frac{{{\rm{ - a}}{{\rm{x}}^2}{\rm{ - ax}}}}{{{x^2} - 1}}\) và \(\frac{{3{\rm{x}}}}{{x - 1}}\)
Hướng dẫn giải
Thảo luận (1)
Ta có: \(\frac{{{\rm{ - a}}{{\rm{x}}^2}{\rm{ - ax}}}}{{{x^2} - 1}} = \frac{{ - a\left( {{x^2} + x} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \frac{{ - ax\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \frac{{{\rm{ - ax}}}}{{x - 1}}\)
Để hai phân thức sau bằng nhau: \(\frac{{{\rm{ - a}}{{\rm{x}}^2}{\rm{ - ax}}}}{{{x^2} - 1}}\) và \(\frac{{3{\rm{x}}}}{{x - 1}}\) khi và chỉ khi a = -3
Trả lời bởi Hà Quang Minh
Ta có: \(\frac{{x - y}}{{{x^3} - {y^3}}} = \frac{{x - y}}{{\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)}} = \frac{1}{{{x^2} + xy + {y^2}}}\)
Trả lời bởi Hà Quang Minh