Cho tam giác ABC có đường cao AH = 6 cm, \(\widehat{B}\) = 40°, \(\widehat{C}\) = 35°.Tính độ dài các đoạn thẳng AB, BH, AC, BC (làm tròn kết quả đến hàng phần mười của centimét).
Bài 2. Một số hệ thức về cạnh và góc trong tam giác vuông
H24
Hướng dẫn giải
Thảo luận (1)
H24
Cho tam giác ABC vuông tại A có \(\widehat{B}\) = 30°.Chứng minh AC = \(\dfrac{1}{2}\)BC.
Hướng dẫn giải
Thảo luận (1)
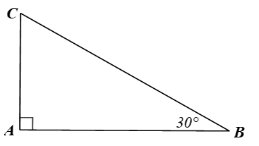
Xét tam giác \(ABC\) vuông tại \(A\), ta có:
\(AC = BC.\sin 30^\circ = \frac{1}{2}BC\).
Trả lời bởi datcoder
H24
Cho tam giác ABC vuông cân tại A. Chứng minh AB = AC = \(\dfrac{\sqrt{2}}{2}BC\).
Hướng dẫn giải
Thảo luận (1)

Do tam giác \(ABC\) vuông cân tại \(A\) nên \(AB = AC\), \(\widehat B = \widehat C = 45^\circ \).
Xét tam giác \(ABC\) vuông cân tại \(A\), ta có:
\(AB = AC = BC.\sin 45^\circ = \frac{{\sqrt 2 }}{2}BC\).
Trả lời bởi datcoder
H24
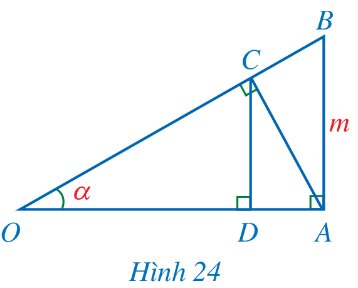
Trong Hình 24, cho \(\widehat{O}=\alpha,AB=m\) và \(\widehat{OAB}=\widehat{OCA}=\widehat{ODC}=90^o\). Chứng minh:
Chứng minh:
a) OA = m.cot α;
b) AC = m.cos α;
c) CD = m.cos2 α.
Hướng dẫn giải
Thảo luận (1)
a) Xét tam giác \(OAB\) vuông tại \(A\) ta có: \(OA = m.\cot \alpha \).
b) Xét tam giác \(OAC\) vuông tại \(C\) ta có:
\(AC = OA.\sin \alpha = m.\cot \alpha .\sin \alpha = m.\frac{{\cos \alpha }}{{\sin \alpha }}.\sin \alpha = m.\cos \alpha \).
c) Xét tam giác \(OAC\) vuông tại \(C\) ta có:
\(OC = OA.\cos \alpha = m.\cot \alpha .\cos \alpha = m.\frac{{\cos \alpha }}{{\sin \alpha }}.\cos \alpha = m.\frac{{{{\cos }^2}\alpha }}{{\sin \alpha }}\).
Xét tam giác \(OCD\) vuông tại \(D\) ta có:
\(CD = OC.\sin \alpha = m.\frac{{{{\cos }^2}\alpha }}{{\sin \alpha }}.\sin \alpha = m.{\cos ^2}\alpha \).
Trả lời bởi datcoder
H24
Tính độ dài đường gấp khúc ABCDEGH (làm tròn kết quả đến hàng phần mười của centimét), biết các tam giác OAB, OBC, OCD, ODE, OEG, OGH là các tam giác vuông tại các đỉnh lần lượt là B, C, D, E, G, H; các góc O1, O2, O3, O4, O5, O6 đều bằng 30° và OA 2 cm (Hình 25).
Đọc tiếp
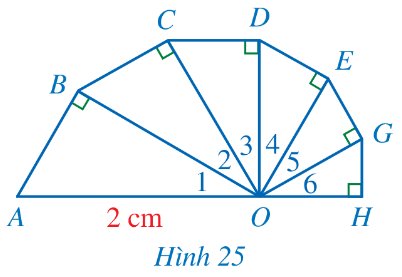
Tính độ dài đường gấp khúc ABCDEGH (làm tròn kết quả đến hàng phần mười của centimét), biết các tam giác OAB, OBC, OCD, ODE, OEG, OGH là các tam giác vuông tại các đỉnh lần lượt là B, C, D, E, G, H; các góc O1, O2, O3, O4, O5, O6 đều bằng 30° và OA = 2 cm (Hình 25).
Hướng dẫn giải
Thảo luận (1)
Xét tam giác \(ABO\) vuông tại \(B\), ta có:
+) \(AB = AO.\sin 30^\circ = 2.\sin 30^\circ = 1\left( {cm} \right)\).
+) \(BO = AO.\cos 30^\circ = 2.\cos 30^\circ = \sqrt 3 \left( {cm} \right)\).
Xét tam giác \(BOC\) vuông tại \(C\), ta có:
+) \(BC = BO.\sin 30^\circ = \sqrt 3 .\sin 30^\circ = \frac{{\sqrt 3 }}{2}\left( {cm} \right)\).
+) \(CO = BO.\cos 30^\circ = \sqrt 3 .\cos 30^\circ = \frac{3}{2}\left( {cm} \right)\).
Xét tam giác \(COD\) vuông tại \(D\), ta có:
+) \(CD = CO.\sin 30^\circ = \frac{3}{2}.\sin 30^\circ = \frac{3}{4}\left( {cm} \right)\).
+) \(DO = CO.\cos 30^\circ = \frac{3}{2}.\cos 30^\circ = \frac{{3\sqrt 3 }}{4}\left( {cm} \right)\).
Xét tam giác \(DOE\) vuông tại \(E\), ta có:
+) \(DE = DO.\sin 30^\circ = \frac{{3\sqrt 3 }}{4}.\frac{1}{2} = \frac{{3\sqrt 3 }}{8}\left( {cm} \right)\).
+) \(EO = DO.\cos 30^\circ = \frac{{3\sqrt 3 }}{4}.\frac{{\sqrt 3 }}{2} = \frac{9}{8}\left( {cm} \right)\).
Xét tam giác \(EOG\) vuông tại \(G\), ta có:
+) \(EG = EO.\sin 30^\circ = \frac{9}{8}.\frac{1}{2} = \frac{9}{{16}}\left( {cm} \right)\).
+) \(GO = EO.\cos 30^\circ = \frac{9}{8}.\frac{{\sqrt 3 }}{2} = \frac{{9\sqrt 3 }}{{16}}\left( {cm} \right)\).
Xét tam giác \(GOH\) vuông tại \(H\), ta có:
\(GH = GO.\sin 30^\circ = \frac{{9\sqrt 3 }}{{16}}.\frac{1}{2} = \frac{{9\sqrt 3 }}{{32}}\left( {cm} \right)\).
Vậy độ dài đường gấp khúc \(ABCDEGH\) là:
\(ABCDEGH = 1 + \frac{{\sqrt 3 }}{2} + \frac{3}{4} + \frac{{3\sqrt 3 }}{8} + \frac{9}{{16}} + \frac{{9\sqrt 3 }}{{32}} = \frac{{37\left( {2 + \sqrt 3 } \right)}}{{32}} \approx 4,3 \left( {cm} \right)\).
Trả lời bởi datcoder
H24
Hình 26 minh hoạ một phần con sông có bề rộng AB = 100 m. Một chiếc thuyền đi thẳng từ vị trí B bên này bờ sông đến vị trí C bên kia bờ sông. Tính quãng đường BC (làm tròn kết quả đến hàng phần mười của mét), biết \(\widehat{ABC}\) = 35°.

Hướng dẫn giải
Thảo luận (1)
Xét tam giác \(ABC\) vuông tại \(A\), ta có:
\(BC = \frac{AB}{\cos 35^\circ} = \frac{100}{\cos 35^\circ} \approx 122,1 \left( m \right)\).
Vậy quãng đường \(BC\) dài \(122,1m\).
Trả lời bởi datcoder
H24
Từ vị trí A ở phía trên một tòa nhà có chiều cao AD 68 m, bác Duy nhìn thấy vị trí C cao nhất của một tháp truyền hình, góc tạo bởi tia AC và tia AH theo phương nằm ngang là widehat{CAH}43^o. Bác Duy cũng nhìn thấy chân tháp tại vị trí B mà góc tạo bởi tia AB và tia AH là widehat{BAH}28^o, điểm H thuộc đoạn thẳng BC (Hình 27). Tính khoảng cách BD từ chân tháp đến chân tòa nhà và chiều cao BC của tháp truyền hình (làm tròn kết quả đến hàng phần mười của mét).
Đọc tiếp
Từ vị trí A ở phía trên một tòa nhà có chiều cao AD = 68 m, bác Duy nhìn thấy vị trí C cao nhất của một tháp truyền hình, góc tạo bởi tia AC và tia AH theo phương nằm ngang là \(\widehat{CAH}=43^o\). Bác Duy cũng nhìn thấy chân tháp tại vị trí B mà góc tạo bởi tia AB và tia AH là \(\widehat{BAH}=28^o\), điểm H thuộc đoạn thẳng BC (Hình 27). Tính khoảng cách BD từ chân tháp đến chân tòa nhà và chiều cao BC của tháp truyền hình (làm tròn kết quả đến hàng phần mười của mét).

Hướng dẫn giải
Thảo luận (1)
Xét tam giác \(ABD\) vuông tại \(D\) ta có:
\(BD = \frac{{AD}}{{\tan 28^\circ }} = \frac{{68}}{{\tan 28^\circ }} \approx 127,9\left( m \right)\).
Vì AHBD là hình chữ nhật nên \(BH = AD = 68m\), \(AH = BD\).
Xét tam giác \(ACH\) vuông tại \(H\) ta có:
\(CH = AH.\tan 43^\circ \approx 127,9.\tan 43^\circ \approx 119,3\left( m \right)\).
Chiều cao \(BC\) của tháp truyền hình là: \(BC = CH + BH \approx 119,3 + 68 = 187,3\left( m \right)\).
Trả lời bởi datcoder
Xét tam giác \(ABH\) vuông tại \(H\), ta có:
+) \(AB = \frac{{AH}}{{\sin 40^\circ }} = \frac{6}{{\sin 40^\circ }} \approx 9,3\left( {cm} \right)\).
+) \(BH = \frac{{AH}}{{\tan 40^\circ }} = \frac{6}{{\tan 40^\circ }} \approx 7,2\left( {cm} \right)\).
Xét tam giác \(AHC\) vuông tại \(H\), ta có:
+) \(AC = \frac{{AH}}{{\sin 35^\circ }} = \frac{6}{{\sin 35^\circ }} \approx 10,5\left( {cm} \right)\).
+) \(CH = \frac{{AH}}{{\tan 35^\circ }} = \frac{6}{{\tan 35^\circ }} \approx 8,6\left( {cm} \right)\).
Ta có: \(BC = BH + HC \approx 7,2 + 8,6 \approx 15,8\left( {cm} \right)\).
Trả lời bởi datcoder