Hình 12 mô tả đường lên dốc ở Hình 11, trong đó góc giữa BC và phương nằm giữa BA là \(\widehat{ABC}=15^o\).
Cạnh góc vuông AC và cạnh huyền BC (Hình 12) có liên hệ với nhau như thế nào?
Cho tam giác ABC vuông tại A (Hình 13).
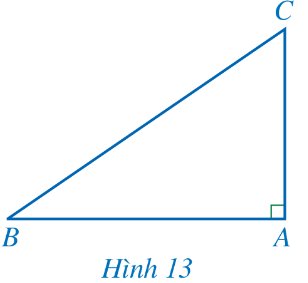
a) Biểu diễn sin B, cos C theo AC, BC.
b) Viết công thức tính AC theo BC và sin B.
c) Viết công thức tính AC theo BC và cos C.
a) \(\sin B = \frac{{AC}}{{BC}}\);\(\cos C = \frac{{AC}}{{BC}}\).
b) \(AC = BC.\sin B\).
c) \(AC = BC.\cos C\).
Trả lời bởi datcoderTính độ cao AC trong Hình 12 khi BC = 20 m (làm tròn kết quả đến hàng phần mười của mét).
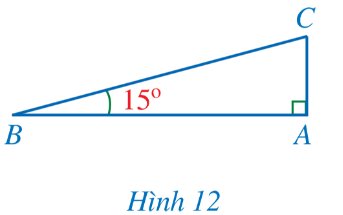
Độ cao AC là:
\(AC = BC.\sin 15^\circ = 20.\sin 15^\circ \approx 5,2\left( m \right)\).
Trả lời bởi datcoderCho tam giác nhọn ABC có đường cao CK. Biểu diễn CK theo AC và sinA. Từ đó, chứng minh diện tích của tam giác ABC bằng \(\dfrac{1}{2}\).AB.AC.sinA.
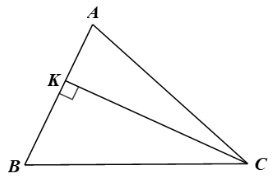
Vì tam giác \(ACK\) vuông tại \(K\) nên: \(CK = AC.\sin A\).
Ta có: \({S_{ABC}} = \frac{1}{2}CK.AB = \frac{1}{2}.AB.AC.\sin A\).
Trả lời bởi datcoderCho tam giác ABC vuông tại A (Hình 17).
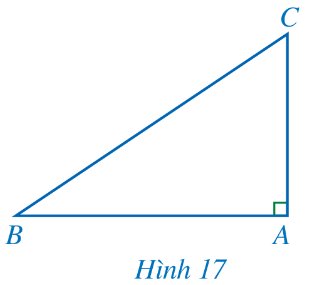
a) Biểu diễn tan B, cot C theo AB, AC.
b) Viết công thức tính AC theo AB và tan B.
c) Viết công thức tính AC theo AB và cot C.
a) Vì tam giác \(ABC\) vuông tại \(A\) nên:
\(\tan B = \frac{{CA}}{{AB}}\);\(\cot C = \frac{{AC}}{{AB}}\).
b) Ta có: \(AC = AB.\tan B\).
c) Ta có: \(AC = AB.\cot C\).
Trả lời bởi datcoderTính độ dài cạnh AB trong Hình 17 khi AC = 4 cm và \(\widehat{B}\) = 34° (làm tròn kết quả đến hàng phần mười của centimét).
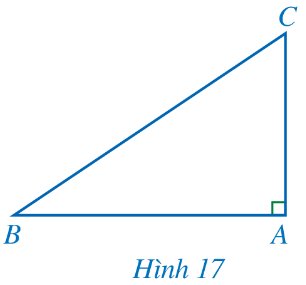
Vì tam giác \(ABC\) vuông tại \(A\) nên:
\(AB = AC.\cot B = 4.\cot 34^\circ \approx 5,9\left( {cm} \right)\).
Trả lời bởi datcoderTìm độ dài cạnh góc vuông AC và số đo các góc nhọn B, C của tam giác vuông ABC, biết cạnh góc vuông AB = 5 cm và cạnh huyền BC = 13 cm.
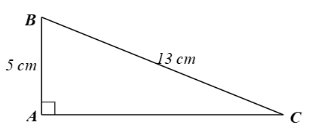
Xét tam giác \(ABC\) vuông tại \(A\), ta có:
+) \(B{C^2} = A{B^2} + A{C^2}\) (theo định lý Pythagore), suy ra \({13^2} = {5^2} + A{C^2}\) hay \(AC = 12\left( {cm} \right)\).
+) \(\cos B = \frac{{AB}}{{BC}} = \frac{5}{{13}}\) suy ra \(\widehat B \approx 67^\circ \).
+) \(\widehat B + \widehat C = 90^\circ \) (tổng hai góc nhọn của tam giác vuông), suy ra \(\widehat C = 90^\circ - \widehat B \approx 90^\circ - 67^\circ = 23^\circ \).
Trả lời bởi datcoderTìm số đo góc nhọn C và độ dài cạnh góc vuông AB, cạnh huyền BC của tam giác vuông ABC, biết cạnh góc vuông AC = 7 cm và \(\widehat{B}\) = 55°.
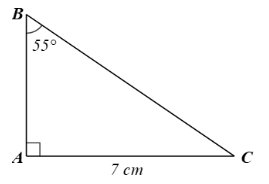
Xét tam giác \(ABC\) vuông tại \(A\), ta có:
+) \(\widehat B + \widehat C = 90^\circ \) (tổng hai góc nhọn của tam giác vuông), suy ra \(\widehat C = 90^\circ - \widehat B = 90^\circ - 55^\circ = 35^\circ \).
+) \(AB = AC.\tan C = 7.\tan 35^\circ \approx 4,9\left( {cm} \right)\).
+) Ta có: \(AC = BC.\sin B\)
suy ra \(BC = \frac{AC}{\sin B} = \frac{7}{\sin 55^\circ} \approx 8,5\left( {cm} \right)\).
Trả lời bởi datcoderCho hình chữ nhật ABCD thoả mãn AC = 6 cm, \(\widehat{BAC}\) = 47°. Tính độ dài các đoạn thẳng AB, AD.
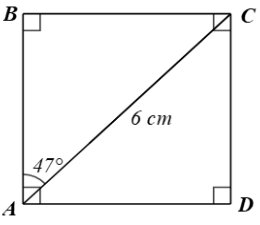
Xét tam giác \(ABC\) vuông tại \(B\) có:
+) \(AB = AC.\cos \widehat {BAC} = 6.\cos 47^\circ \approx 4,1\left( {cm} \right)\).
+) \(BC = AC.\sin \widehat {BAC} = 6.\sin 47^\circ \approx 4,4\left( {cm} \right)\).
Do \(ABCD\) là hình chữ nhật nên \(BC = AD\) (tính chất hình chữ nhật) suy ra \(AD \approx 4,4\left( {cm} \right)\).
Trả lời bởi datcoderTìm x, y trong mỗi hình 23a, 23b, 23c (làm tròn kết quả đến hàng phần mười của centimét).
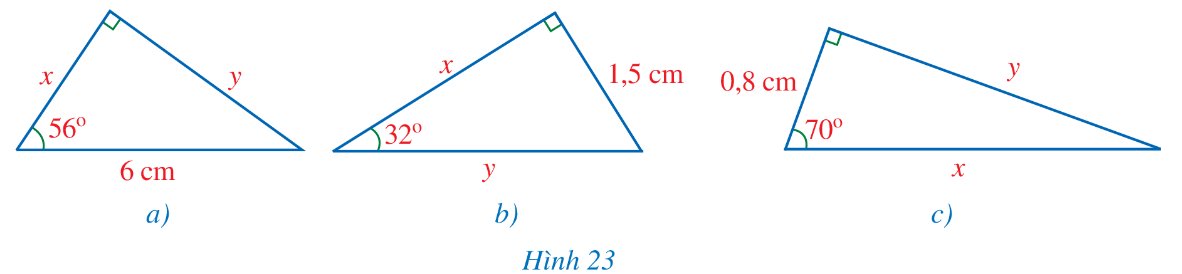
a) Ta có:
+) \(x = 6.\cos 56^\circ \approx 3,4\left( {cm} \right)\).
+) \(y = 6.\sin 56^\circ \approx 5\left( {cm} \right)\).
b) Ta có:
+) \(x = \frac{{1,5}}{{\tan 32^\circ }} \approx 2,4\left( {cm} \right)\).
+) \(y = \frac{{1,5}}{{\sin 32^\circ }} \approx 2,8\left( {cm} \right)\).
c) Ta có:
+) \(y = 0,8.\tan 70^\circ \approx 2,2\left( {cm} \right)\).
+) \(x = \frac{{0,8}}{{\cos 70^\circ }} \approx 2,3\left( {cm} \right)\).
Trả lời bởi datcoder
Cạnh góc vuông \(AC\) và cạnh huyền \(BC\) liên hệ với nhau dựa vào \(\sin B = \frac{AC}{BC}\) hay \(\sin 15^\circ = \frac{AC}{BC}\)
suy ra \(AC = BC.sin 15^\circ\)
Trả lời bởi datcoder