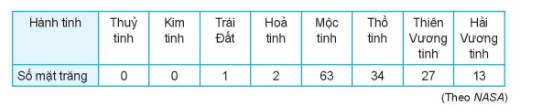
Hãy chọn số đặc trưng đo xu thế trung tâm của mỗi mẫu số liệu sau. Giải thích và tinh giá trị của số đặc trưng đó.a) Số mặt trăng đã biết của các hành tinh: b) Số đường chuyền thành công trong một trận đấu của một số cầu thủ bóng đá:32 24 20 14 23.c) Chỉ số IQ của một nhóm học sinh:801028310310894110106104100d) Các sai số trong một phép đo: 10 15 18 15 14 13 42 15 12 14 42.
Đọc tiếp
Hãy chọn số đặc trưng đo xu thế trung tâm của mỗi mẫu số liệu sau. Giải thích và tinh giá trị của số đặc trưng đó.
a) Số mặt trăng đã biết của các hành tinh:
b) Số đường chuyền thành công trong một trận đấu của một số cầu thủ bóng đá:
32 24 20 14 23.
c) Chỉ số IQ của một nhóm học sinh:
| 80 | 102 | 83 | 103 | 108 | 94 | 110 | 106 | 104 | 100 |
d) Các sai số trong một phép đo: 10 15 18 15 14 13 42 15 12 14 42.
Hướng dẫn giải
Thảo luận (1)
a) Sắp xếp lại số liệu:
0 0 1 2 13 27 34 63
Trung vị là \(\dfrac{(2+13)}{2}=7,5.\)
Ta không chọn số trung bình vì số trung bình là 17,5 chênh lệch với 63 lớn. Mốt cũng thế.
b) Các số liệu bài cho không chênh lệch quá lớn với số trung bình nên ta chọn số trung bình.
Số đường truyền trung bình là: \(\dfrac{{32 + 24 + 20 + 14 + 23}}{5} = 22,6\)
c) Các số liệu bài cho không chênh lệch quá lớn với số trung bình nên ta chọn số trung bình.
IQ trung bình là \(\frac{{80 + {\kern 1pt} 102 + {\kern 1pt} 83 + {\kern 1pt} 103 + {\kern 1pt} 108 + {\kern 1pt} 94 + {\kern 1pt} 110 + {\kern 1pt} 106 + {\kern 1pt} 104 + {\kern 1pt} 100}}{{10}} = 99\)
d) Ta thấy có hai giá trị 42 chênh lệch lớn với các số còn lại nên ta chọn Mốt để đo xu thế trung tâm.
Mốt là 15 (tần số là 3).
Chú ý
Mẫu dữ liệu có sự chênh lệch quá lớn thì không nên chọn số trung bình để đo xu thế trung tâm.
Trả lời bởi Hà Quang Minh