Bài 1. Tỉ số lượng giác của góc nhọn

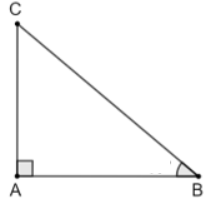
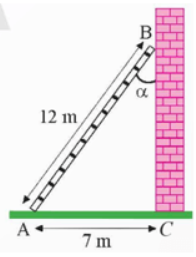
a)

Các tỉ số lượng giác của góc \(\alpha \) là:

sin \(\alpha \) = \(\frac{{BC}}{{AC}} \approx 0,64\)

cos \(\alpha \) = \(\frac{{AB}}{{AC}} \approx 0,77\)

tan \(\alpha \) = \(\frac{{BC}}{{AB}} \approx 0,84\)

cot \(\alpha \) = \(\frac{1}{{\tan \alpha }} \approx 1,19\)

b) 

Các tỉ số lượng giác của góc \(\widehat {BAC}\) là:

sin \(\widehat {BAC}\) = \(\frac{{BC}}{{AC}} = \frac{4}{5}\)

cos \(\widehat {BAC}\) = \(\frac{{AB}}{{AC}} = \frac{3}{5}\)

tan \(\widehat {BAC}\) = \(\frac{{BC}}{{AB}} = \frac{4}{3}\)

cot \(\widehat {BAC}\) = \(\frac{1}{{\tan \alpha }} = \frac{3}{4}\)

Các tỉ số lượng giác của góc \(\widehat {ACB}\) là:

sin \(\widehat {ACB}\) = \(\frac{{AB}}{{AC}} = \frac{3}{5}\)

cos \(\widehat {ACB}\) = \(\frac{{BC}}{{AC}} = \frac{4}{5}\)

tan \(\widehat {ACB}\) = \(\frac{{AB}}{{BC}} = \frac{3}{4}\)

cot \(\widehat {ACB}\) = \(\frac{1}{{\tan \widehat {BAC}}} = \frac{4}{3}\) 

Sử dụng thước đo góc, ta đo được \(\widehat {BAC} \approx 53^\circ\) và \(\widehat {ACB} \approx 37^\circ\). Kiểm tra lại các tỉ số lượng giác bằng máy tính cầm tay, ta thấy các giá trị bằng với giá trị mình viết phía trên.

a) BC = 5 cm; AB = 3 cm.

Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:

\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{5^2} - {3^2}} = 4\)

Các tỉ số lượng giác của \(\widehat {ABC}\) và \(\widehat {ACB}\) là:

sin \(\widehat {ABC}\) = cos \(\widehat {ACB}\) = \(\frac{{AC}}{{BC}} = \frac{4}{5} = 0,8\)

cos \(\widehat {ABC}\) = sin \(\widehat {ACB}\) = \(\frac{{AB}}{{BC}} = \frac{3}{5} = 0,6\)

tan \(\widehat {ABC}\) = cot \(\widehat {ACB}\) = \(\frac{{AC}}{{AB}} = \frac{4}{3} \approx 1,33\)

cot \(\widehat {ABC}\) = tan \(\widehat {ACB}\) = \(\frac{1}{{\tan \widehat {ABC}}} = \frac{3}{4} = 0,75\)

b) BC = 13cm; AC = 12 cm

Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:

\(AB = \sqrt {B{C^2} - A{C^2}} = \sqrt {{{13}^2} - {{12}^2}} = 5\)

Các tỉ số lượng giác của \(\widehat {ABC}\) và \(\widehat {ACB}\) là:

sin \(\widehat {ABC}\) = cos \(\widehat {ACB}\) = \(\frac{{AC}}{{BC}} = \frac{{12}}{{13}} \approx 0,92\)

cos \(\widehat {ABC}\) = sin \(\widehat {ACB}\) = \(\frac{{AB}}{{BC}} = \frac{5}{{13}} \approx 0,38\)

tan \(\widehat {ABC}\) = cot \(\widehat {ACB}\) = \(\frac{{AC}}{{AB}} = \frac{{12}}{5} = 2,4\)

cot \(\widehat {ABC}\) = tan \(\widehat {ACB}\) = \(\frac{1}{{\tan \widehat {ABC}}} = \frac{5}{{12}} \approx 0,42\)

c) BC = \(5\sqrt 2 \) cm; AB = 5 cm

Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:

\(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{(5\sqrt 2 )}^2} - {5^2}} = 5\)

Các tỉ số lượng giác của \(\widehat {ABC}\) và \(\widehat {ACB}\) là:

sin \(\widehat {ABC}\) = cos \(\widehat {ACB}\) = \(\frac{{AC}}{{BC}} = \frac{5}{{5\sqrt 2 }} = \frac{\sqrt 2}{{2 }} \approx 0,71\)

cos \(\widehat {ABC}\) = sin \(\widehat {ACB}\) = \(\frac{{AB}}{{BC}} = \frac{5}{{5\sqrt 2 }} = \frac{\sqrt 2}{{2 }} \approx 0,71\)

tan \(\widehat {ABC}\) = cot \(\widehat {ACB}\) = \(\frac{{AC}}{{AB}} = \frac{5}{5} = 1\)

cot \(\widehat {ABC}\) = tan \(\widehat {ACB}\) = \(\frac{1}{{\tan \widehat {ABC}}} = 1\)

d) AB = \(a\sqrt 3 \); AC = a

Áp dụng định lí Pythagore vào tam giác vuông ABC, ta có:

\(BC = \sqrt {A{C^2} + A{B^2}} = \sqrt {{a^2} + {{\left( {a\sqrt 3 } \right)}^2}} = 2a\)

Các tỉ số lượng giác của \(\widehat {ABC}\) và \(\widehat {ACB}\) là:

sin \(\widehat {ABC}\) = cos \(\widehat {ACB}\) = \(\frac{{AC}}{{BC}} = \frac{{a}}{{2a}} = \frac{{1 }}{2} = 0,5\)

cos \(\widehat {ABC}\) = sin \(\widehat {ACB}\) = \(\frac{{AB}}{{BC}} = \frac{{a\sqrt 3 }}{{2a}} = \frac{{\sqrt 3 }}{2} \approx 0,87\)

tan \(\widehat {ABC}\) = cot \(\widehat {ACB}\) = \(\frac{{AC}}{{AB}} = \frac{a}{{a\sqrt 3 }} = \frac{\sqrt 3}{{3 }}\approx 0,58\)

cot \(\widehat {ABC}\) = tan \(\widehat {ACB}\) = \(\frac{1}{{\tan \widehat {ABC}}} = \sqrt 3 \approx 1,73 \)

a) \(A = \frac{{\sin {{30}^o}.\cos {{30}^o}}}{{\cot {{45}^o}}} = \frac{{\frac{1}{2}.\frac{{\sqrt 3 }}{2}}}{1} = \frac{{\sqrt 3 }}{4} \approx 0,43\)

b) \(B = \frac{{\tan {{30}^o}}}{{\cos {{45}^o}.\cos {{60}^o}}} = \frac{{\frac{{\sqrt 3 }}{3}}}{{\frac{{\sqrt 2 }}{2}.\frac{1}{2}}} = \frac{{2\sqrt 6 }}{3} \approx 1,63\) 

a) sin 60^o = cos (90^o – 60^o) = cos 30^o

b) cos 75^o = sin (90^o – 75^o) = sin 15^o

c) tan 80^o = cot (90^o – 80^o) = cot 10^o

a) Ta có:

\(\begin{array}{l}sin{26^o} \approx 0,44;\\\cos {26^o} \approx 0,9;\\\tan {26^o} \approx 0,49;\\\cot {26^o} \approx 2,05\end{array}\)

b) Ta có:

\(\begin{array}{l}sin{72^o} \approx 0,95;\\\cos {72^o} \approx 0,31;\\\tan {72^o} \approx 3,08;\\\cot {72^o} \approx 0,32\end{array}\)

c) Ta có:

\(\begin{array}{l}sin{81^o}27' \approx 0,99;\\\cos {81^o}27' \approx 0,15;\\\tan {81^o}27' \approx 6,65;\\\cot {81^o}27' \approx 0,15\end{array}\) 

a) \(\alpha \) = \({53^o}8'\)

b) \(\alpha \) = \({36^o}52'\) 

Theo đề bài ta có tam giác vuông sau:

Ta có tan \(\alpha = \frac{{AB}}{{AC}} = \frac{{21}}{{15}} = \frac{7}{5}\)

Sử dụng máy tính cầm tay, ta được góc \(\alpha  \approx {54^o}\).

Ta có sin \(\alpha \) = \(\frac{{BC}}{{AC}} = \frac{7}{{12}}\).

Sử dụng máy tính cầm tay, ta được góc \(\alpha \) \( \approx {35^o}41'\).