So sánh:
a) \(\sqrt{\dfrac{4}{3}}\) và \(\sqrt{\dfrac{3}{4}}\); b) \(\sqrt{0,48}\) và 0,7;
c) \(\sqrt[3]{-45}\) và \(\sqrt[3]{-50}\); d) \(-10\) và \(\sqrt[3]{-999}\).
Chứng minh:
a) \(\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)=1\); b) \(\left(\sqrt[3]{2}+1\right)\left[\left(\sqrt[3]{2}\right)^2-\sqrt[3]{2}+1\right]=3\).
a. Ta có:
\(\left( {2 - \sqrt[{}]{3}} \right)\left( {2 + \sqrt[{}]{3}} \right) = {2^2} - {\left( {\sqrt[{}]{3}} \right)^2} = 4 - 3 = 1\).
b. Ta có:
\(\left( {\sqrt[3]{2} + 1} \right)\left[ {{{\left( {\sqrt[3]{2}} \right)}^2} - \sqrt[3]{2} + 1} \right] = {\left( {\sqrt[3]{2}} \right)^3} + {1^3} = 2 + 1 = 3\).
Trả lời bởi datcoderTính độ dài cạnh huyền của mỗi tam giác vuông trong Hình 2.
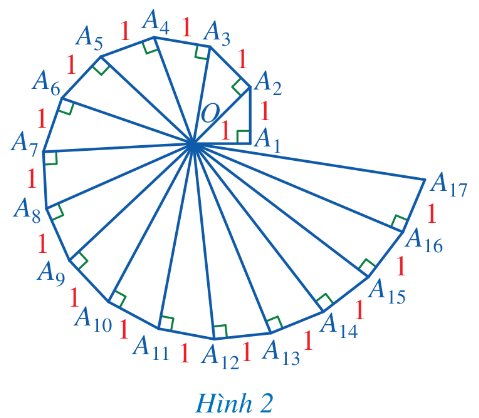
\(O{A_2} = \sqrt {1_{}^2 + 1_{}^2} = \sqrt 2 \).
\(OA_3^{} = \sqrt {\left( {\sqrt 2 } \right)_{}^2 + 1_{}^2} = \sqrt 3 \).
\(OA_4^{} = \sqrt {\left( {\sqrt 3 } \right)_{}^2 + 1_{}^2} = 2\).
\(OA_5^{} = \sqrt {2_{}^2 + 1_{}^2} = \sqrt 5 \).
=> \(OA_n^{} = \sqrt n \).
\(OA_6^{} = \sqrt 6 ,\) \(OA_7^{} = \sqrt 7 ,OA_8^{} = \sqrt 8 ,\) \(OA_9^{} = 3,\) \(OA_{10}^{} = \sqrt {10} ,\) \(OA_{11}^{} = \sqrt {11} ,OA_{12}^{} = \sqrt {12} ,\) \(\,OA_{13}^{} = \sqrt {13} \), \(OA_{14}^{} = \sqrt {14} ,\) \(OA_{15}^{} = \sqrt {15} ,\) \(OA_{16}^{} = 4,\) \(OA_{17}^{} = \sqrt {17} \).
Trả lời bởi datcoderĐại Kim tự tháp Giza là Kim tự tháp Ai Cập lớn nhất và là lăng mộ của Vương triều thứ Tư của pharaoh Khufu. Nền kim tự tháp có dạng hình vuông với diện tích khoảng 53 052 m2 (Nguồn: https://vi.wikipedia.org). Hỏi độ dài cạnh của nền kim tự tháp đó là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Gọi độ dài nền của kim tự tháp đó là a (m, a > 0)
Ta có: \({a^2} = 53052\) nên \(a \approx 230,3\,\,\left( m \right)\).
Vậy độ dài nền của kim tự tháp đó là \(230,3\left( m \right)\).
Trả lời bởi datcoderGiông bão thổi mạnh, một cây bị gãy gập xuống làm ngọn cây chạm đất và tạo với phương nằm ngang một góc 45° (minh họa ở Hình 3). Người ta đo được khoảng cách từ chỗ ngọn cây chạm đất đến gốc cây là 4,5 m. Giả sử cây mọc vuông góc với mặt đất, hãy tính chiều cao của cây đó theo đơn vị mét (làm tròn kết quả đến hàng phần mười).
Gọi các điểm biểu diễn như hình vẽ.
Xét tam giác ABC vuông tại A có \(\widehat C = 45^\circ\) nên tam giác ABC vuông cân tại A.
Suy ra AB = AC = 4,5m.
Chiều cao phần ngọn bị gãy BC là: \(BC = \sqrt{AB^2+AC^2} = \sqrt{4,5^2 + 4,5^2} = \frac{9\sqrt2}{2} \approx 6,4(m)\)
Vậy chiều cao của cây là: \(AB + BC \approx 4,5 +6,4 = 10,9 (m)\)
Trả lời bởi datcoderThể tích của một khối bê tông có dạng hình lập phương là khoảng 220 348 cm3. Hỏi độ dài cạnh của khối bê tông đó là bao nhiêu cetimét (làm tròn kết quả đến hàng phần mười)?
Gọi độ dài cạnh của khối bê tông là a (cm, a > 0).
Ta có: \({a^3} = 220348\) nên \(a \approx 60,4\)(cm).
Vậy độ dài cạnh của khối bê tông đó là 60,4 (cm).
Trả lời bởi datcoder
a. Do \(\frac{4}{3} > \frac{3}{4}\) nên \(\sqrt[{}]{{\frac{4}{3}}} > \sqrt[{}]{{\frac{3}{4}}}\).
b. Ta có: \(0,7 = \sqrt[{}]{{0,49}}\). Do \(0,48 < 0,49\) nên \(\sqrt[{}]{{0,48}} < \sqrt[{}]{{0,49}}\) hay \(\sqrt[{}]{{0,48}} < 0,7\).
c. Do \( - 45 > - 50\) nên \(\sqrt[3]{{ - 45}} > \sqrt[3]{{ - 50}}\).
d. Ta có: \( - 10 = \sqrt[3]{{ - 1000}}\). Do \( - 1000 < - 999\) nên \(\sqrt[3]{{ - 1000}} < \sqrt[3]{{ - 999}}\) hay \( - 10 < \sqrt[3]{{ - 999}}\).
Trả lời bởi datcoder