Học tại trường
Chưa có thông tin
Đến từ
Bắc Giang , Chưa có thông tin
Số lượng câu hỏi
70
Số lượng câu trả lời
1
Điểm GP
0
Điểm SP
0
Người theo dõi (10)
Đang theo dõi (3)
DL
Trong hình sau, khi lật ô tiếp theo thì điều gì sẽ xảy ra?
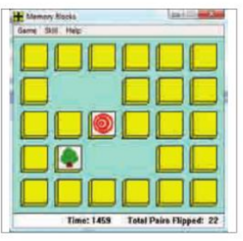
| Ba ô được lật | |
| Hai ô đã lật bị úp lại, ô mới được lật | |
| Không có gì xảy ra |