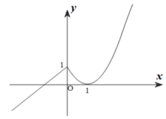
Học tại trường
Chưa có thông tin
Đến từ
Thừa Thiên Huế , Chưa có thông tin
Số lượng câu hỏi
53
Số lượng câu trả lời
41
Điểm GP
0
Điểm SP
21
Người theo dõi (36)
Đang theo dõi (4)
NQ
Câu trả lời:
Có vì đó là sự chuyển thể từ thể rắn sang thể lỏng
NQ
Câu trả lời:
Hiện tượng không liên quan là Sự Tạo Thành Hơi Nước