Cho tam giác ABC có đường trung tuyến CE. G là điểm thuộc cạnh CE sao cho \(GC=\dfrac{2}{3}CE\).
Gọi K, D, I lần lượt là trung điểm của AG, AC và GC.
Khi đó, khẳng định nào dưới đây là sai?
G là trọng tâm tam giác ABC.AI là đường trung tuyến ứng với đỉnh A của tam giác AGC.BD, AI, CK đồng quy.AG là đường cao của tam giác ABC.Hướng dẫn giải: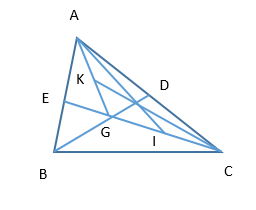
Dựa vào cách xác định điểm G suy ra G là trọng tâm tam giác ABC.
Suy ra AG là đường trung tuyến của tam giác ABC.
Dễ dàng chứng minh được AI, CK, GD là ba đường trung tuyến của tam giác GAC nên AI, CK, GD đồng quy tại một điểm.
