Cho \(\Delta ABC\) vuông tại \(A\), \(M\) là trung điểm \(AC\). Gọi \(D,E\) là hình chiếu của \(A\) và \(C\) xuống đường thẳng \(BM\). So sánh \(AB\) và \(BD+BE\)?
\(BD+BE>2AB\).\(BD+BE< 2AB\).\(BD+BE=2AB\).\(BD+BE< AB\).Hướng dẫn giải: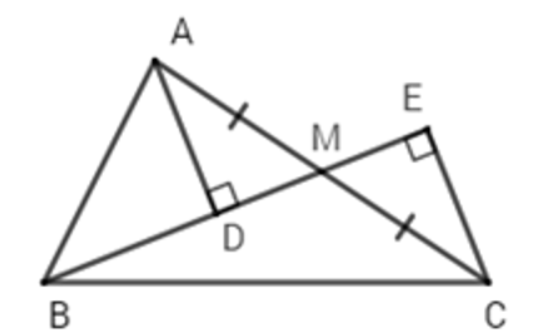
Do \(\Delta ABM\) vuông tại A (gt) nên BA<BM (quan hệ giữa đường vuông góc và đường xiên)
Mà BM=BD+DM \(\Rightarrow\) BA < BD+DM (1)
Lại có: BM=BE-ME \(\Rightarrow\) BA < BE-ME (2)
Cộng 2 vế của (1) và (2) ta được: 2BA < BD+BE+MD-ME
Do M là trung điểm của AC nên AM = MC
Ta suy ra \(\Delta ADM=\Delta CEM\) (cạnh huyền - góc nhọn)
\(\Rightarrow\) MD = ME \(\Rightarrow\) MD - ME = 0
Do đó 2BA < BD+BE hay BD+BE > 2BA
