Cho \(\Delta ABC\) có \(\widehat{C}=90^0\), \(AC< BC\). Kẻ \(CH\perp AB\). Trên cạnh \(AB,AC\) lấy \(M,N\) sao cho \(BM=BC,CN=CH\). Chọn câu đúng nhất
\(MN\perp AC\).\(AC+BC< AB+CH\).Cả 2 đều đúng.Cả 2 đều sai.Hướng dẫn giải: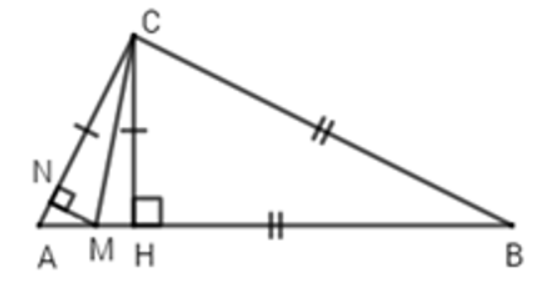
Có \(BM=BC\) \(\Rightarrow\Delta BMC\) cân tại B
\(\Rightarrow\widehat{MCB}=\widehat{CMB}\) (1)
Lại có: \(\left\{{}\begin{matrix}\widehat{MCB}+\widehat{MCA}=\widehat{ACB}=90^0\\\widehat{CMH}+\widehat{MCH}=90^0\end{matrix}\right.\) (2)
Từ (1) và (2) \(\Rightarrow\) \(\widehat{MCH}=\widehat{MCN}\)
Khi đó ta chứng minh được \(\Delta MHC=\Delta MNC\) (c.g.c)
\(\Rightarrow\widehat{MHC}=\widehat{MNC}=90^0\) \(\Rightarrow MN\perp AC\)
Xét \(\Delta AMN\) có \(AN\) là đường vuông góc còn \(AM\) là đường xiên hạ từ A xuống MN nên AM > AN (quan hệ giữa đường vuông góc và đường xiên)
Ta có: \(\left\{{}\begin{matrix}BM=BC\\CH=CN\\AM>AN\end{matrix}\right.\) \(\Rightarrow BM+AM+CH>BC+CN+AN\) \(\Rightarrow AB+CH>BC+AC\) hay \(AC+BC< AB+CH\)
