Các dạng toán liên quan đến giao thoa sóng
Nội dung lý thuyết
Các phiên bản khácCÁC DẠNG TOÁN LIÊN QUAN ĐẾN GIAO THOA SÓNG
Các bài toán về giao thoa sóng, người ta thường xét trong trường hợp hai nguồn cùng pha (trường hợp 2 nguồn ngược pha rất hiếm gặp, các trường hợp khác như 2 nguồn dao động vuông pha hoặc độ lệch pha bất kì thì bạn không cần phải quan tâm).
Để đơn giản, ta xét hai nguồn dao động cùng pha có phương trình là: \(u_1=u_2=A\cos(\omega t)\)
1. Tìm số điểm dao động với biên độ cực đại, cực tiểu giữa hai nguồn
*Cách 1: Tính theo điều kiện cực đại, cực tiểu
- Điểm M dao động với biên độ cực đại suy ra \(d_2-d_1=k\lambda\)
- Ta có: \(d_2+d_1=S_1S_2\)
\(\Rightarrow d_2=\dfrac{k\lambda+S_1S_2}{2}\) với \(0< d_2 < S_1S_2\)
\(\Rightarrow 0< \dfrac{k\lambda+S_1S_2}{2} < S_1S_2\)(1)
Các giá trị \(k\) thoả mãn phương trình (1) là số điểm dao động với biên cực đại.
- Điểm M dao động với biên độ cực tiểu cũng làm tương tự như trên với điều kiện \(d_2-d_1=(k+0,5)\lambda\)
*Cách 2 (Sử dụng công thức tính nhanh): Ta biết rằng, khoảng cách giữa hai điểm cực đại liên tiếp trên đoạn \(S_1S_2\) là \(\dfrac{\lambda}{2}\). Do vậy ý tưởng là ta tính số khoảng nguyên trên \(OS_1\), chính là số cực đại trên khoảng \(OS_1\) rồi nhân đôi (cả trên \(OS_2\) cũng như vậy) rồi cộng với trung điểm \(O\).
- Kết quả ta tìm được:
+ Các điểm dao động với biên cực đại là: \(\boxed{2.[\dfrac{S_1S_2}{\lambda}]+1}\)
+ Các điểm dao động với biên cực tiểu là: \(\boxed{2.[\dfrac{S_1S_2}{\lambda}+0,5]}\)
Trong đó, \([x]\) là phép lấy phần nguyên của \(x\). Ví dụ: \([8,1]=8\); \([8,9]=8\)
*Ví dụ: Hai nguồn sóng kết hợp S1, S2 cùng biên độ và cùng pha, cách nhau 58cm, có tần số sóng là 5Hz. Tốc độ truyền sóng là 40cm/s. Tìm số cực đại, cực tiểu giao thoa trên đoạn S1S2.
Giải:
Bước sóng: \(\lambda=\dfrac{v}{f}=\dfrac{40}{5}=8cm\)
Số cực đại giao thoa: \(2.[\dfrac{S_1S_2}{\lambda}]+1=2.[\dfrac{58}{8}]+1=2.7+1=15\)
Số cực tiểu giao thoa: \(2.[\dfrac{S_1S_2}{\lambda}+0,5]=2.[\dfrac{58}{8}+0,5]=2.7=14\)
2. Tìm số điểm dao động với biên độ cực đại, cực tiểu giữa hai điểm bất kì
Bài toán là: Tìm số điểm dao động với biên độ cực đại (cực tiểu) trên đoạn MN.
Nhận xét:
+ Ta lấy điểm P thuộc đoạn MN dao động với biên độ cực đại, khi đó P thoả mãn: \(d_2-d_1=k.\lambda\)
+ Khi P di chuyển từ M đến N thì hệ số k giảm dần, do đó ta có: \(\boxed{MS_1-MS_1\ge k.\lambda \ge NS_2-NS_1}\)(*)
Giải bất phương trình (*), số giá trị nguyên của \(k\) thoả mãn (*) chính là số điểm cực đại cần tìm.
+ Tìm các điểm cực tiểu cũng làm tương tự.
Ví dụ: Tại 2 điểm A, B trên mặt chất lỏng cách nhau 20cm có hai nguồn phát sóng kết hợp dao động theo phương trình \(u_1 = 4\cos(20\pi t)\) (mm); \(u_2 = 4\cos(20\pi t + \pi)\) (mm). Tốc độ truyền sóng trên mặt nước là 40cm/s. Gọi C và D là hai điểm trên mặt chất lỏng sao cho ABCD là hình chữ nhật, khoảng cách từ CD đến AB là 15cm. Tìm số điểm dao động với biên độ cực đại trên đoạn DC.
Giải:
\(AC=DB=\sqrt{15^2+20^2}=25cm\)
Tần số: \(f=\dfrac{\omega}{2\pi}=\dfrac{20\pi}{2\pi}=10(Hz)\)
Bước sóng: \(\lambda=v/f=40/10=4cm\)
Điểm \(P\) thuộc đoạn \(AC\) dao động với biên độ cực đại \(\Rightarrow d_2-d_1=k\lambda\)
Có: \(DB-DA\ge d_2-d_1\ge CB-CA\)
\(\Rightarrow 25-15\ge k.4 \ge 15-25\)
\(\Rightarrow 10\ge k.4 \ge -10\)
\(\Rightarrow 2,5 \ge k \ge -2,5\)
\(k\) nguyên \(\Rightarrow k = -2;-1;0;1;2\)
Có 5 giá trị \(k\) thoả mãn, nên trên đoạn CD có 5 điểm dao động với biên độ cực đại.
3. Các điểm nằm trên đường trung trực của đoạn thẳng nối hai nguồn
Điểm M nằm trên trung trực đoạn \(S_1S_2\), cách đều 2 nguồn một khoảng là \(d\)
Phương trình dao động của 2 nguồn là: \(u_1=u_2=A\cos(\omega t)\)
Phương trình sóng do \(S_1\) đến \(M\) là: \(u_{1M}=A\cos(\omega t-\dfrac{2\pi d}{\lambda})\)
Phương trình sóng do \(S_2\) đến \(M\) là: \(u_{2M}=A\cos(\omega t-\dfrac{2\pi d}{\lambda})\)
Phương trình dao động của \(M\) là: \(u_M=u_{1M}+u_{2M}=2A\cos(\omega t-\dfrac{2\pi d}{\lambda})\)
Nhận xét:
- Điểm \(M\) dao động trễ pha so với hai nguồn là: \(\Delta \varphi = \dfrac{2\pi d}{\lambda}\)
- Điểm \(M\) lệch pha so với \(N\) là: \(\Delta \varphi' = \dfrac{2\pi (d-d')}{\lambda}\)
Tương tự như bài Độ lệch pha của hai điểm trên phương truyền sóng, ta cũng có kết quả:
- Điểm \(M\) cùng pha với nguồn khi \(\boxed{d=k\lambda}\), ngược pha khi \(\boxed{d=(k+0,5)\lambda}\), vuông pha khi \(\boxed{d=(k+0,5)\dfrac{\lambda}{2}}\)
- Điểm \(M\) cùng pha với \(N\) khi \(\boxed{d-d'=k\lambda}\), ngược pha khi: \(\boxed{d-d'=(k+0,5)\lambda}\), vuông pha khi \(\boxed{d-d'=(k+0,5)\dfrac{\lambda}{2}}\)
Ví dụ: Trên mặt thoáng của chất lỏng có hai nguồn kết hợp A và B cách nhau 20cm với phương trình dao động: \(u_1= u_2 = cos(\omega t)\) cm. Bước sóng \(\lambda = 8\)cm. Biên độ sóng không đổi. Gọi M là một điểm trên đường trung trực của AB dao động cùng pha với các nguồn A, B và gần trung điểm H của AB nhất. Tính khoảng cách HM.
Giải:
Từ bài toán trên ta đã có kết quả: Điểm M nằm trên đường trung trực cách các nguồn một khoảng \(d\) sẽ dao động cùng pha với các nguồn khi và chỉ khi: \(d=k\lambda\).
Ta có: AH = 10 cm, λ = 8 cm
\(\Rightarrow d=k.8\)
Lại có \(d>AH\Rightarrow 8k>10\Rightarrow k>1,25\)(1)
Điểm \(M\) gần \(H\) nhất nên \(k\) là số nguyên nhỏ nhất thảo mãn (1) \(\Rightarrow k = 2\) \(\Rightarrow d = 8.2=16cm\)
\(\Rightarrow MH = \sqrt{16^2-10^2}=\sqrt{156}cm\)
4. Các điểm gần nhất, xa nhất
Đây là dạng toán có tính chất suy luận, tuỳ từng tình huống bài toán mà ta có những lập luận hợp lí.
Ví dụ ta có hệ vân giao thoa như hình vẽ:
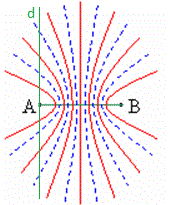
Đường thẳng d vuông góc với AB tại A. Đề bài yêu cầu tìm điểm M thuộc d dao động với biên độ cực đại và gần A nhất thì nhìn vào hình vẽ ta thấy điểm M thuộc vân cực đại ngoài cùng. Nếu đề yêu cầu tìm điểm M thuộc d vào động với biên độ cực đại và xa A nhất thì M thuộc vân cực đại đầu tiên (kể từ trung trực).
Ví dụ: Trên bề mặt chất lỏng có hai nguồn kết hợp A, B cách nhau 40 cm dao động cùng pha. Biết sóng do mỗi nguồn phát ra có tần số f = 10 Hz, vận tốc truyền sóng 2 m/s. Gọi M là một điểm nằm trên đường thẳng Δ vuông góc với AB tại A và M dao động với biên độ cực đại. Tìm giá trị lớn nhất của đoạn AM.
Giải:
Bước sóng: \(λ = v/f = 200/10 = 20\) (cm)
Vì M cách xa điểm A nhất nên M chính là giao điểm của Δ với đường hyperbol cực đại số 1.
Gọi \(d_1 = AM; d_2 = BM\):
Áp dụng định lý Pi-ta-go ta có: \(d_2^2-d_1^2=AB^2 \) hay \(d_2^2-d_1^2=40^2\,\)(1)
Vì M nằm trên đường hyperbol cực đại số 1 nên ta có: \(d_2-d_1=\lambda\) hay \(d_2-d_1=20\)(2)
Giải hệ phương trình gồm (1) và (2) ta được \(AM = d_1 = 30\) (cm).