Bài 4: Khối lượng riêng. Áp suất chất lỏng
Nội dung lý thuyết
Các phiên bản khácI. Khối lượng riêng
Khối lượng riêng của một chất là khối lượng của một đơn vị thể tích chất đó.
\(\rho=\dfrac{m}{V}\)
Trong đó, ρ, m, V lần lượt là kí hiệu khối lượng riêng, khối lượng, thể tích.
Đơn vị của khối lượng riêng trong hệ SI là kg/m3.
| Chất rắn | ρ (kg/m3) | Chất lỏng | ρ (kg/m3) | Chất khí | ρ (kg/m3) |
| Chì | 11 300 | Thủy ngân | 13 500 | Carbonic | 1,98 |
| Đồng | 8 900 | Nước | 999 | Oxygen | 1,43 |
| Thép | 7 800 | Xăng | 700 | Hydrogen | 0,09 |
Khối lượng riêng của một số chất ở điều kiện bình thường về nhiệt độ và áp suất
Khối lượng riêng là một thuộc tính của các chất, có thể đo được qua phép đo khối lượng và thể tích.
@2801745@
II. Áp lực và áp suất
1. Áp lực

Khi đứng trên sàn, bàn chân của ta tác dụng áp lực (lực ép vuông góc) lên sàn. Lực này tác dụng lên mọi điểm thuộc diện tích bị ép giữa bàn chân và mặt sàn.
Tác dụng của áp lực lên mặt ép càng mạnh khi cường độ của áp lực càng lớn và diện tích mặt bị ép càng nhỏ.
2. Áp suất
Để đặc trưng cho tác dụng của áp lực, người ta dùng khái niệm áp suất, có độ lớn bằng áp lực chia cho diện tích bị ép.
\(p=\dfrac{F}{S}\)
Đơn vị của áp suất là N/m2, có tên gọi là pascal (Pa). Ngoài ra, áp suất còn được đo bằng một số đơn vị như atmosphere (atm), mmHg,… theo liên hệ:
1 atm = 760 mmHg ≈ 105 Pa
@2801841@
III. Áp suất của chất lỏng
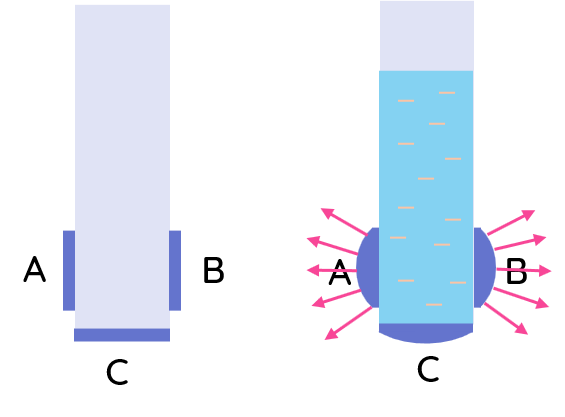
Chất lỏng gây áp suất không chỉ lên đáy bình chứa mà còn lên thành bình và lên mọi điểm trong chất lỏng.
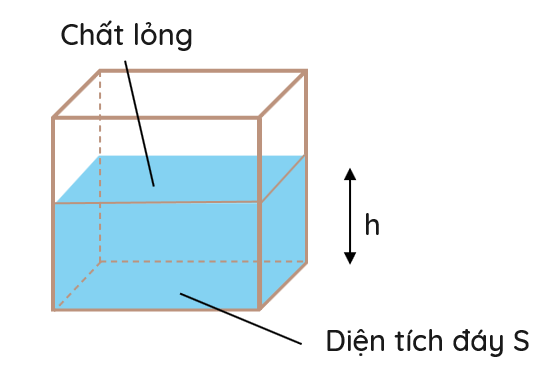
Mỗi điểm ở độ sâu h trong lòng chất lỏng sẽ có áp suất là:
\(p=p_0+\rho gh\)
Trong đó p0 là áp suất khí quyển.
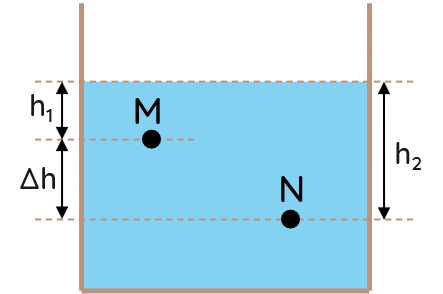
Độ chênh lệch về áp suất của chất lưu giữa hai điểm M và N có độ sâu h1 và h2 so với mặt thoáng của chất lưu đứng yên.
\(\Delta p=\rho g\Delta h\)
Phương trình trên được gọi là phương trình cơ bản của chất lưu đứng yên.
1. Công thức tính khối lượng riêng: \(\rho=\dfrac{m}{V}\)
2. Công thức tính áp suất: \(p=\dfrac{F}{S}\)
3. Công thức tính áp suất của chất lỏng: \(p=p_0+\rho gh\)
4. Phương trình cơ bản của chất lưu đứng yên: \(\Delta p=\rho g\Delta h\)