Bài 2. Chuyển động thẳng đều

CHUYỂN ĐỘNG THẲNG ĐỀU

1. Tốc độ trung bình

  \({{v}_{tb}}=\dfrac{s}{t}\)

\(s\) = x₂ - x₁: quãng đường vật đi được trong thời gian t

\(t\) = t₂ - t₁ : thời gian vật chuyển động trên quãng đường s

➤ Tốc độ trung bình cho biết mức độ nhanh, chậm của chuyển động

2. Chuyển động thẳng đều

Chuyển động thẳng đều là chuyển động có quỹ đạo là đường thẳng và có tốc độ trung bình như nhau trên mọi quãng đường.

3. Quãng đường đi trong chuyển động thẳng đều

Trong chuyển động thẳng đều, quãng đường đi được \(s\) tỉ lệ thuận với thời gian chuyển động \(t\)

      \(s=vtb.t=v.t\)

II. Phương trình chuyển động và đồ thị tọa độ- thời gian của chuyển động thẳng đều

1. Phương trình của chuyển động thẳng đều

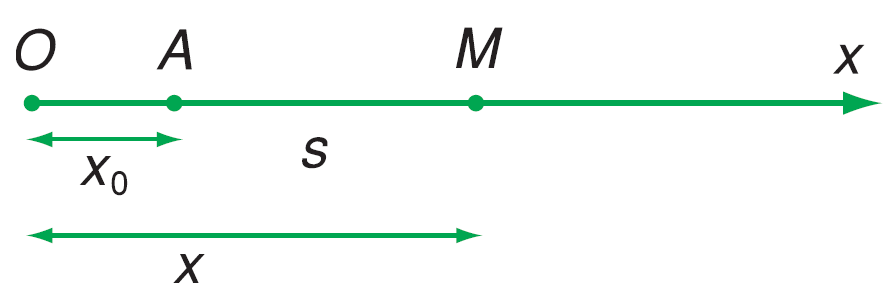
Giả sử có chất điểm \(M\) xuất phát từ điểm \(A\) trên đường thẳng \(Ox\) với vận tốc \(v\)

Điểm \(A\) các gốc tọa độ \(O\) một đoạn là \(OA=x_0\)

Lấy mốc thời gian là lúc chất điểm bắt đầu chuyển động, tọa độ của chất điểm sau thời gian \(t\) là

\(x=x_0+s=x_0+vt\)

Phương trình trên được gọi là phương trình của chuyển động thẳng đều.

2. Đồ thị toạ độ – thời gian của chuyển động thẳng đều

- Có dạng là một đường thẳng, biểu diễn sự phụ thuộc của tọc độ của vật chuyển động vào thời gian

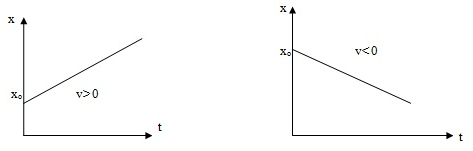
- Cách vẽ đồ thị tọa độ - thời gian của một chuyển động thẳng đều:

• Lập bảng giá trị (x, t) có ít nhất là 2 giá trị: một giá trị ứng với thời điểm ban đầu (thường chọn là t = 0) và một giá trị ứng với thời điểm t lúc sau bất kì
• Vẽ hai trục vuông góc (trục hoành là trục thời gian Ot và trục tung là trục tọa độ Ox). Dựa vào bảng giá trị (x, t), xác định hai điểm trên đồ thị. Nối từ điểm thứ nhất (ứng với điểm ban đầu) kéo dài qua điểm thứ hai ta được đồ thị tọa độ - thời gian của chuyển động

- Ví dụ: Vẽ đồ thị của chuyển động thẳng đều có phương trình: \(x=10+20t\) (với x tính bằng km và t tính bằng giờ)