§4. Các tập hợp số
Nội dung lý thuyết
Các phiên bản khácI. CÁC TẬP HỢP SỐ ĐÃ HỌC
1. Tập hợp các số tự nhiên \(N\)
\(N=\left\{0,1,2,3,4,...\right\}\)
\(N\)*\(=\left\{1,2,3,4,...\right\}\)
2. Tập hợp các số nguyên \(Z\)
\(Z=\left\{...,-3,-2,-1,0,1,2,3,...\right\}\)
Các số \(-1,-2,-3,...\) là các số nguyên âm.
Vậy \(Z\) gồm các số tự nhiên và các số nguyên âm.
3. Tập hợp các số hữu tỉ \(Q\)
- Số hữu tỉ biểu diễn được dưới dạng một phân số \(\dfrac{a}{b}\), trong đó \(a,b\in Z;b\ne0\).
Ví dụ: \(5;-\dfrac{3}{8};\dfrac{45}{4};....\) là các số hữu tỉ.
- Hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\) biểu diễn cùng một số hữu tỉ khi và chỉ khi \(ad=bc\).
Ví dụ: +) \(\dfrac{2}{3}=\dfrac{10}{15}\) (do \(2.15=3.10=30\))
+) \(\dfrac{11}{4}=\dfrac{33}{12}\) (do \(11.12=4.33=132\))
- Số hữu tỉ còn biểu diễn được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.
Ví dụ: \(\dfrac{5}{4}=1,25\) ;
\(\dfrac{5}{12}=0,41\left(6\right)\) ; ...
4. Tập hợp các số thực \(R\)
Tập hợp các số thực gồm các số thập phân hữu hạn, vô hạn tuần hoàn và vô hạn không tuần hoàn. Các số thập phân vô hạn không tuần hoàn gọi là các số vô tỉ.
Ví dụ: \(\alpha=0,101101110...\) (số chữ số 1 sau mỗi chữ số 0 tăng dần) là một số vô tỉ.
Tập hợp các số thực bao gồm các số hữu tỉ và các số vô tỉ.
Mỗi số thực được biểu diễn bởi một điểm trên trục số và ngược lại.
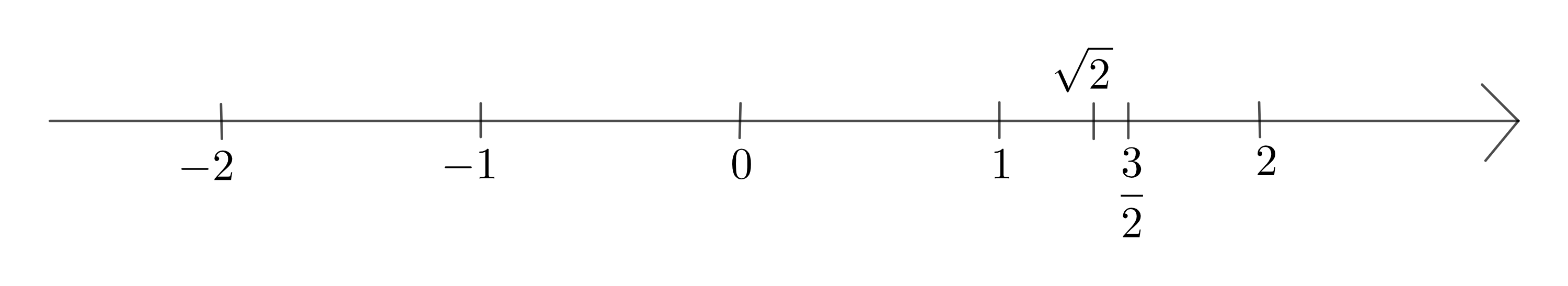
II. CÁC TẬP HỢP CON THƯỜNG DÙNG CỦA R
Trong toán học ta thường gặp các tập hợp con sau đây của tập hợp các số thực \(R\):
+) Khoảng:
| \(\left(a;b\right)=\left\{x\in R|a< x< b\right\}\) |
|
| \(\left(a;+\infty\right)=\left\{x\in R|a< x\right\}\) |
|
| \(\left(-\infty;b\right)=\left\{x\in R|x< b\right\}\) |
|
+) Đoạn:
| \(\left[a;b\right]=\left\{x\in R|a\le x\le b\right\}\) |
|
+) Nửa khoảng:
| \([a;b)=\left\{x\in R|a\le x< b\right\}\) |
|
| \((a;b]=\left\{x\in R|a< x\le b\right\}\) |
|
| \([a;+\infty)=\left\{x\in R|a\le x\right\}\) |
|
| \((-\infty;b]=\left\{x\in R|x\le b\right\}\) |
|
@1835228@
Ví dụ 1: Xác định các tập hợp sau:
a) \([-3;1)\cup(0;4]\)
b) \(\left(-7;-4\right)\cap\left(4;7\right)\)
c) \(\left(-2;3\right)\)\\([1;5)\)
Giải:
a) \([-3;1)\cup(0;4]=\left[-3;4\right]\)
b) \(\left(-7;-4\right)\cap\left(4;7\right)=\varnothing\)
c) \(\left(-2;3\right)\)\\([1;5)\) = \(\left(-2;1\right)\)
@1835450@
Ví dụ 2: Cho 2 tập hợp \(A=\left\{x\in R|2x-5< 3+4x\right\}\) và \(B=\left\{x\in R|7x+6\le6x+7\right\}\)
Tìm các phần tử nguyên của tập hợp \(A\cap B\).
Giải:
Ta có: \(A=\left\{x\in R|2x-5< 3+4x\right\}=\left\{x\in R|x>-4\right\}=\left(-4;+\infty\right)\)
\(B=\left\{x\in R|7x+6\le6x+7\right\}=\left\{x\in R|x\le1\right\}=(-\infty;1]\)
Do đó \(A\cap B=\left(-4;+\infty\right)\cap(-\infty;1]=(-4;1]\)
Các phần tử nguyên thuộc tập hợp \((-4;1]\) là: \(-3;-2;-1;0;1\).
@1835076@






