Một cuốn sách khổ 17 × 24 cm, tức là chiều rộng 17 cm, chiều dài 24 cm. Gọi α là góc giữa đường chéo và cạnh 17 cm. Tính sin α, cos α (làm tròn đến chữ số thập phân thứ hai) và tính số đo α (làm tròn đến độ).
Luyện tập chung trang 79
H24
Hướng dẫn giải
Thảo luận (1)
H24
Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết HB = 3 cm, HC = 6 cm, \(\widehat{HCA}\) = 60°. Hãy tính độ dài các cạnh (làm tròn đến cm), số đo các góc của tam giác ABC (làm tròn đến độ).
Hướng dẫn giải
Thảo luận (1)
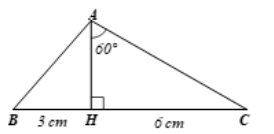
Cạnh \(BC = BH + HC = 3 + 6 = 9\) cm
Ta có:
\(\sin \widehat {HAC} = \frac{{HC}}{{AC}}\) hay \(\sin {60^0} = \frac{6}{{AC}}\) hay \(AC = \frac{6}{{\sin {{60}^0}}} = 4\sqrt 3 \approx 7\) cm
\(\tan \widehat {HAC} = \frac{{HC}}{{AH}}\) hay \(\tan {60^0} = \frac{6}{{AH}}\) nên \(AH = \frac{6}{{\tan {{60}^0}}} = 2\sqrt 3 \) cm
\(\widehat C = 90^\circ - 60^\circ = 30^\circ\)
Tam giác ABH vuông tại H nên ta có:
\(A{B^2} = A{H^2} + B{H^2} = {\left( {2\sqrt 3 } \right)^2} + {3^2} = 21\) hay \(AB = \sqrt {21} \approx 5\) cm (vì \(AB > 0\))
Ta có: \(tan B = \frac{AH}{BH} = \frac{2\sqrt 3}{3}\) suy ra \( \widehat B \approx 49^\circ\)
Áp dụng định lí tổng ba góc trong một tam giác, ta có:
\(\widehat {BAC} = 180^\circ - (\widehat B + \widehat C) = 180^\circ - (49^\circ + 30^\circ) = 101^\circ\)
Trả lời bởi datcoder
H24
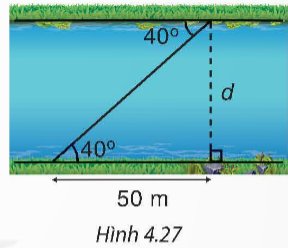
Tìm chiều rộng d của dòng sông trong Hình 4.27 (làm tròn đến m).
Hướng dẫn giải
Thảo luận (1)
Chiều rộng của sông là \(d = 50.\tan {40^0} \approx 42\) m
Vậy chiều rộng của sông khoảng 42 m
Trả lời bởi datcoder
H24
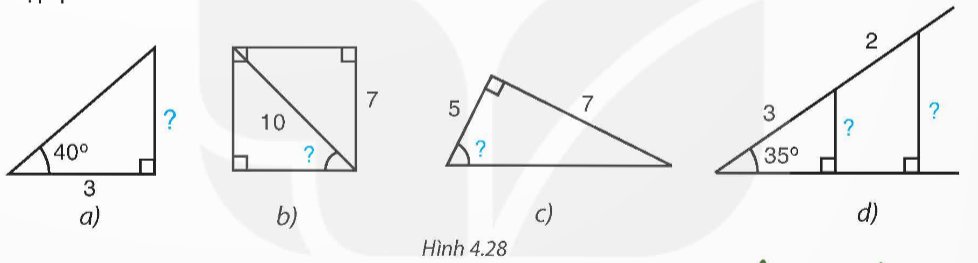
Tính các số liệu còn thiếu (dấu "?") ở Hình 4.28 với góc làm tròn đến độ, với độ dài làm tròn đến chữ số thập phân thứ nhất.
Hướng dẫn giải
Thảo luận (1)
a) Vị trí dấu hỏi chấm là \(3.\tan {40^0} \approx 2,5\)
b)
Gọi \(\alpha \) là góc ở vị trí dấu ?
Ta có \(\sin \alpha = \frac{7}{{10}}\) nên \(\alpha \approx {44^0}\)
c)
Gọi \(\alpha \) là góc ở vị trí dấu ?
Ta có \(\tan \alpha = \frac{7}{5}\) nên \(\alpha \approx {54^0}\)
d)
Gọi độ dài cạnh góc vuông nhỏ hơn là a, cạnh góc vuông lớn hơn là b
Ta có \(a = 3.\sin {35^0} \approx 1,7\)
\(b = \left( {3 + 2} \right).\sin {35^0} \approx 2,9\)
Trả lời bởi datcoder
H24
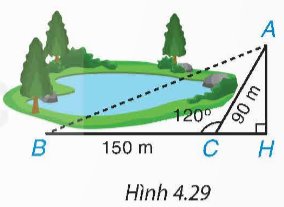
Một bạn muốn tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước. Biết rằng các khoảng cách từ một điểm C đến A và đến B là CA = 90 m, CB = 150 m và \(\widehat{ACB}\) = 120° (H.4.29). Hãy tính AB giúp bạn.
Hướng dẫn giải
Thảo luận (1)
Ta có: \(\widehat {BCA} + \widehat {ACH} = {180^0}\) (kề bù) suy ra \(\widehat {ACH} = 180^\circ - \widehat {BCA} = 180^\circ - 120^\circ = 60^\circ\)
Nên \(AH = AC.\sin \widehat {ACH} = 90.\sin 60 = 45\sqrt 3 \) m
\(CH = AC.\cos \widehat {ACH} = 90.\cos {60^0} = 45\) m
Do đó \(BH = BC + CH = 150 + 45 = 195\) m
Tam giác ABH vuông tại H nên \(A{B^2} = A{H^2} + B{H^2}\) (định lý Pythagore)
Thay số ta có \(A{B^2} = {\left( {45\sqrt 3 } \right)^2} + {195^2}= 44100\) hay \(AB = 210\) m.
Trả lời bởi datcoder
H24
Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30). Chiều rộng của mặt trên AB của đập là 3 m. Độ dốc của sườn AD, tức là tanD 1,25. Độ dốc của sườn BC, tức là tanC 1,5. Chiều cao của đập là 3,5 m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).
Đọc tiếp
Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30). Chiều rộng của mặt trên AB của đập là 3 m. Độ dốc của sườn AD, tức là tanD = 1,25. Độ dốc của sườn BC, tức là tanC = 1,5. Chiều cao của đập là 3,5 m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).
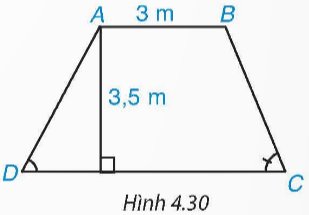
Hướng dẫn giải
Thảo luận (1)
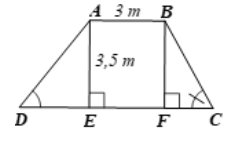
Kẻ BK vuông góc với DC tại K và AH vuông góc với DC tại H nên hình thang có hai đường cao là AH và BK; AB= HK = 3,5 m
Xét tứ giác ABKH có AH // BK; AH = BK; \(\widehat {AHK} = {90^0}\)
Nên ABKH là hình chữ nhật suy ra HK = AB = 3 m
Tam giác ADH vuông tại H nên ta có:
\(\tan \widehat D = \frac{{AH}}{{DH}}\) hay \(1,25 = \frac{{3,5}}{{DH}}\) suy ra \(DH = \frac{{3,5}}{{1,25}} = 2,8\) m = 28 dm.
\(A{D^2} = D{H^2} + A{H^2} = 3,{5^2} + 2,{8^2} = 20,09\) hay \(AD = \sqrt {20,09} \approx 4,5\) m = 45 dm (vì \(AD > 0\))
Tam giác BKC vuông tại K nên ta có:
\(\tan \widehat C = \frac{{BK}}{{KC}}\) hay \(1,5 = \frac{{3,5}}{{KC}}\) suy ra \(KC = \frac{{3,5}}{{1,5}} = \frac{7}{3} \approx 2,3\) m = 23 dm.
\(B{C^2} = B{K^2} + K{C^2} = 3,{5^2} + 2,{3^2} = 17,54\) hay \(BC = \sqrt {17,54} \approx 4,2\) m =42 dm (vì \(BC > 0\))
Độ dài cạnh DC là \(DC = DH + HK + KC \approx 2,8 + 3 + 2,3 = 8,1m \approx 81dm\)
Trả lời bởi datcoder
H24
Trong một buổi tập trận, một tàu ngầm đang ở trên mặt biển bắt đầu di chuyển theo đường thẳng tạo với mặt nước biển một góc 21° để lặn xuống (H.4.31).a) Khi tàu chuyển động theo hướng đó và đi được 200 m thì tàu ở độ sâu bao nhiêu so với mặt nước biển? (làm tròn đến m).b) Giả sử tốc độ của tàu là 9 km/h thì sau bao lâu (tính từ lúc bắt đầu lặn) tàu ở độ sâu 200 m (tức là cách mặt nước biển 200 m)?
Đọc tiếp
Trong một buổi tập trận, một tàu ngầm đang ở trên mặt biển bắt đầu di chuyển theo đường thẳng tạo với mặt nước biển một góc 21° để lặn xuống (H.4.31).
a) Khi tàu chuyển động theo hướng đó và đi được 200 m thì tàu ở độ sâu bao nhiêu so với mặt nước biển? (làm tròn đến m).
b) Giả sử tốc độ của tàu là 9 km/h thì sau bao lâu (tính từ lúc bắt đầu lặn) tàu ở độ sâu 200 m (tức là cách mặt nước biển 200 m)?
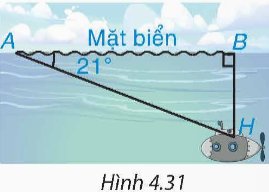
Hướng dẫn giải
Thảo luận (1)
a) Tàu ở độ sâu là \(BH = AH.\sin \widehat A = 200.\sin {21^0} \approx 72\) m
Vậy khi di chuyển được 200 m thì tàu ở độ sâu khoảng 72 m.
b) Ta có \(\sin \widehat A = \frac{{BH}}{{AH}}\) hay \(\sin {21^0} = \frac{{200}}{{AH}}\) suy ra \(AH = \frac{{200}}{{\sin {{21}^0}}} \approx 558\) m = 0,558 km
Thời gian tàu chạy ở độ sâu 200 m là \(0,558:9 = 0,062\) giờ
Trả lời bởi datcoder
Xét cuốn sách có dạng là hình chữ nhật chiều dài \(AB = CD = 24\) cm; chiều rộng \(AC = BD = 17\) cm.
Tam giác ACD vuông tại C có \(A{D^2} = A{C^2} + C{D^2}\) (định lý Pythagore)
Thay số ta có: \(A{D^2} = {17^2} + {24^2} = 865\) hay \(AD = \sqrt {865} \) cm (vì \(AD > 0\))
\(\sin \alpha = \frac{{CD}}{{AD}} = \frac{{24}}{{\sqrt {865} }} \approx 0,82;\cos \alpha = \frac{{AC}}{{AD}} = \frac{{17}}{{\sqrt {865} }} \approx 0,58\) và \(\alpha \approx {55^0}\)
Trả lời bởi datcoder