Cho hai tam giác ABC và DEF thoả mãn \(AB = DE,AC = DF,\widehat {BAC} = \widehat {EDF} = {60^\circ },BC = 6\;{\rm{cm}},\widehat {ABC} = {45^\circ }\). Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD.
Luyện tập chung trang 74
QL
Hướng dẫn giải
Thảo luận (1)
QL
Cho hai tam giác ABC và DEF thoả mãn \(AB = DE\), \(\widehat {ABC} = \widehat {DEF} = {70^\circ },\widehat {BAC} = \widehat {EDF} = {60^\circ },AC = 6\;{\rm{cm}}.\)
Tính độ dài cạnh DF.
Hướng dẫn giải
Thảo luận (1)
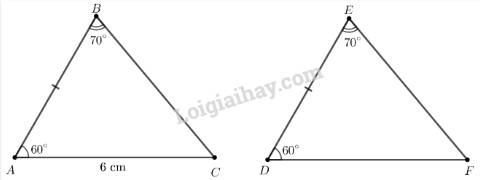
Xét hai tam giác ABC và DEF có:
\(\begin{array}{l}\widehat {ABC} = \widehat {DEF} (= {70^\circ })\\AB = DE\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)
\( \Rightarrow \Delta ABC{\rm{ = }}\Delta DEF\)(g.c.g)
\( \Rightarrow DF = AC\)( 2 cạnh tương ứng)
Mà AC = 6 cm
\( \Rightarrow DF = 6cm\)
Trả lời bởi Kiều Sơn Tùng
QL
Cho Hình 4.44, biết \(EC = ED\) và \(\widehat {AEC} = \widehat {AED}\). Chứng minh rằng:
\(\begin{array}{*{20}{l}}{{\rm{ a) }}\Delta AEC = \Delta AED;}&{{\rm{ b) }}\Delta ABC = \Delta ABD.}\end{array}\)
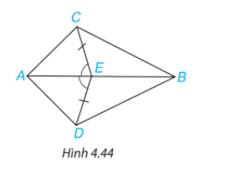
Hướng dẫn giải
Thảo luận (1)
a)Xét hai tam giác AEC và AED có
\(EC = ED\)
\(\widehat {CEA} = \widehat {DEA}\)
AE chung
\( \Rightarrow \Delta AEC{\rm{ = }}\Delta AED\)(c.g.c)
b)
Do \(\Delta AEC{\rm{ = }}\Delta AED\) nên \(\widehat {CAE} = \widehat {DAE}\) ( 2 góc tương ứng) và AC=AD ( 2 cạnh tương ứng).
Xét \(\Delta ABC\) và \(\Delta ABD\) có:
AB chung
\(\widehat {CAE} = \widehat {DAE}\)
AC=AD
\( \Rightarrow \Delta ABC = \Delta ABD\)(c.g.c)
Trả lời bởi Hà Quang Minh
QL
Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A,B,C lần lượt thuộc các tia Ox, Oy, Oz sao cho \(\widehat {CAO} = \widehat {CBO}.\)
a) Chứng minh rằng \(\Delta OAC = \Delta OBC\).
b) Lấy điểm \(M\) trên tia đối của tia CO. Chứng minh rằng \(\Delta MAC = \Delta MBC\).
Hướng dẫn giải
Thảo luận (1)
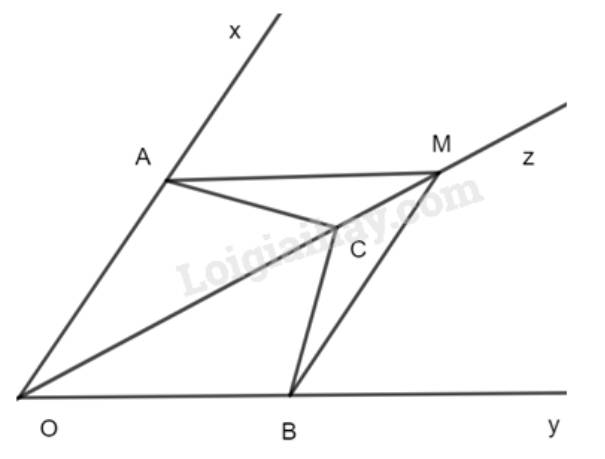
a) Trong \(\Delta OAC\) có: \(\widehat {AOC}+\widehat {OAC}+\widehat {OCA}=180^0\)
Trong \(\Delta OBC\) có: \(\widehat {BOC}+\widehat {OBC}+\widehat {OCB}=180^0\)
Mà \(\widehat {AOC} = \widehat {BOC}\)(do Oz là phân giác góc xOy) và \(\widehat {CAO}=\widehat {CBO}\)
Do đó, \(\widehat {OCA}=\widehat {OCB}\).
Xét \(\Delta OAC\) và \(\Delta OBC\) có:
\(\widehat {AOC} = \widehat {BOC}\) (cmt)
OC chung
\(\widehat {OCA} = \widehat {OCB}(cmt)\)
\(\Rightarrow \Delta OAC = \Delta OBC\)(g.c.g)
b) Do \(\Delta OAC = \Delta OBC\) nên AC=BC ( 2 cạnh tương ứng)
Vì \(\widehat {ACO}\) và \(\widehat {ACM}\) kề bù
\(\widehat {BCO}\) và \(\widehat {BCM}\) kề bù
Mà \(\widehat {ACO} = \widehat {BCO}\) nên \(\widehat {ACM} = \widehat {BCM}\)
Xét \(\Delta MAC\) và \(\Delta MBC\) có:
AC=BC (cmt)
\(\widehat {ACM} = \widehat {BCM}\) (cmt)
CM chung
\( \Rightarrow \Delta MAC = \Delta MBC\)(c.g.c)
Trả lời bởi Kiều Sơn Tùng
Xét hai tam giác ABC và DEF có:
\(\begin{array}{l}AB = DE\\AC = DF\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)
\(\Rightarrow \Delta ABC = \Delta DEF\)(c.g.c)
Do đó:
\(BC=EF = 6cm\) ( 2 cạnh tương ứng)
\( \widehat {ABC} =\widehat {DEF}= {45^o}\) (2 góc tương ứng)
\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\\ \Rightarrow {60^o} + {45^o} + \widehat {ACB} = {180^o}\\ \Rightarrow \widehat {ACB} = {75^o}\end{array}\)
\( \Rightarrow \widehat {EFD} = \widehat {ACB} = {75^o}\)
Trả lời bởi Kiều Sơn Tùng