Bác An đầu tư 1,2 tỉ đồng vào ba loại trái phiếu, trái phiếu chính phủ với lãi suất 7% một năm, trái phiếu ngân hàng với lãi suất 8% một năm và trái phiếu doanh nghiệp rủi ro cao với lãi suất 12% một năm. Vì lí do giảm thuế, bác An muốn số tiền đầu tư trái phiếu chính phủ gấp ít nhất 3 lần số tiền đầu tư trái phiếu ngân hàng. Hơn nữa, để giảm thiểu rủi ro, bác An đầu tư không quá 200 triệu đồng cho trái phiếu doanh nghiệp. Hỏi bác An nên đầu tư mỗi loại trái phiếu bao nhiêu tiền để lợi nhuận thu được sau một năm là lớn nhất?
Bài tập cuối chương II
QL
Bác An đầu tư 1,2 tỉ đồng vào ba loại trái phiếu, trái phiếu chính phủ với lãi suất 7% một năm, trái phiếu ngân hàng với lãi suất 8% một năm và trái phiếu doanh nghiệp rủi ro cao với lãi suất 12% một năm. Vì lí do giảm thuế, bác An muốn số tiền đầu tư trái phiếu chính phủ gấp ít nhất 3 lần số tiền đầu tư trái phiếu ngân hàng. Hơn nữa, để giảm thiểu rủi ro, bác An đầu tư không quá 200 triệu đồng cho trái phiếu doanh nghiệp. Hỏi bác An nên đầu tư mỗi loại trái phiếu bao nhiêu tiền để lợi nhuận thu...
Đọc tiếp
Hướng dẫn giải
Thảo luận (2)
QL
Một công ty dự định chi tối đa 160 triệu đồng cho quảng cáo một sản phẩm mới trong một tháng trên các đài phát thanh và truyền hình. Biết cùng một thời lượng quảng cáo, số người mới quan tâm đến sản phẩm trên truyền hình gấp 8 lần trên đài phát thanh, tức là quảng cáo trên truyền hình có hiệu quả gấp 8 lần trên đài phát thanh.Đài phát thanh chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 900 giây với chi phí là 80 nghìn đồng/giây. Đài truyền hình chỉ nhận các quảng cáo có tổn...
Đọc tiếp
Một công ty dự định chi tối đa 160 triệu đồng cho quảng cáo một sản phẩm mới trong một tháng trên các đài phát thanh và truyền hình. Biết cùng một thời lượng quảng cáo, số người mới quan tâm đến sản phẩm trên truyền hình gấp 8 lần trên đài phát thanh, tức là quảng cáo trên truyền hình có hiệu quả gấp 8 lần trên đài phát thanh.
Đài phát thanh chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 900 giây với chi phí là 80 nghìn đồng/giây. Đài truyền hình chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 360 giây với chi phí là 400 nghìn đồng/giây.
Công ty cần đặt thời gian quảng cáo trên các đài phát thanh và truyền hình như thế nào để hiệu quả nhất?
Gợi ý. Nếu coi hiệu quả khi quảng cáo 1 giây trên đài phát thanh là 1 (đơn vị) thì hiệu quả khi quảng cáo 1 giây trên đài truyền hình là 8 (đơn vị). Khi đó hiệu quả quảng cáo x (giây) trên đài phát thanh và y (giây) trên truyền hình là F(x, y) = x + 8y. Ta cần tìm giá trị lớn nhất của hàm F(x, y) với x, y thoả mãn các điều kiện trong đề bài.
Hướng dẫn giải
Thảo luận (1)
Tham khảo:
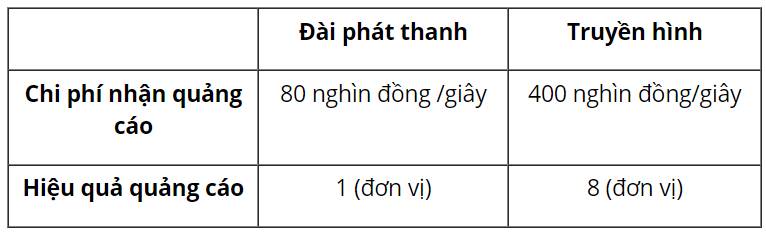
Gọi x và y là số giây quảng cáo trên đài phát thanh và trên truyền hình.
Khi đó \(x \ge 0;y \ge 0\)
160 triệu đồng=160000 (nghìn đồng)
Chi phí quảng cáo x giây trên đài phát thanh và y giây trên truyền hình là \(80x + 400y\)(nghìn đồng)
Vì công ty dự chi tối đa 160 triệu đồng nên ta có
\(80x + 400y \le 160000\)\( \Leftrightarrow x + 5y \le 2000\)
Đài phát thanh chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 900 giây nên ta có: \(x \le 900\)
Đài truyền hình chỉ nhận các quảng cáo có tổng thời lượng trong một tháng tối đa là 360 giây nên ta có: \(y \le 360\)
Ta có hệ bất phương trình:
\(\left\{ {\begin{array}{*{20}{l}}
{x \ge 0}\\
{y \ge 0}\\
{x + 5y \le 2000}\\
{x \le 900}\\
{y \le 360}
\end{array}} \right.\)
Xác định miền nghiệm là miền ngũ giác OABCD với:
A(900;0); B(900;220); C(200;360); D(0;360)
Hiệu quả quảng cáo là: \(F\left( {x;y} \right) = x + 8y\)
Ta có:
\(F\left( {0;0} \right) = 0\)
\(F\left( {900;0} \right) = 900 + 8.0 = 900\)
\(F\left( {900;220} \right) = 900 + 8.220 = 2660\)
\(F\left( {200;360} \right) = 3080\)
\(F\left( {0;360} \right) = 2880\)
Vậy công ty cần đặt thời gian quảng cáo trên đài phát thanh là 200 giây và trên truyền hình là 360 giây thì hiệu quả nhất.
Trả lời bởi Kiều Sơn Tùng
QL
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x - y < - 3\\2y \ge - 4\end{array} \right.\). Điểm nào sau đây thuộc miền nghiệm của hệ đã cho?
A. (0;0)
B. (-2;1)
C. (3;-1)
D. (-3;1)
Hướng dẫn giải
Thảo luận (1)
Thay tọa độ điểm (0;0) vào ta được: \(\left\{ \begin{array}{l}0 - 0 < - 3\left( {ktm} \right)\\2.0 \ge - 4\left( {tm} \right)\end{array} \right.\)
=> Loại A
Thay tọa độ điểm (-2;1) vào ta được: \(\left\{ \begin{array}{l} - 2 - 1 < - 3\left( {ktm} \right)\\2.1 \ge - 4\left( {tm} \right)\end{array} \right.\)
=> Loại B.
Thay tọa độ điểm (3;-1) vào ta được: \(\left\{ \begin{array}{l}3 - \left( { - 1} \right) < - 3\left( {ktm} \right)\\2.\left( { - 1} \right) \ge - 4\left( {tm} \right)\end{array} \right.\)
Loại C
Thay tọa độ điểm (-3;1) vào ta được: \(\left\{ \begin{array}{l} - 3 - 1 < - 3\left( {tm} \right)\\2.1 \ge - 4\left( {tm} \right)\end{array} \right.\)
Chọn D.
Trả lời bởi Hà Quang Minh
QL
Biểu diễn miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}y - 2x \le 2\\y \le 4\\x \le 5\\x + y \ge - 1\end{array} \right.\) trên mặt phẳng tọa độ.
Từ đó tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F\left( {x;y} \right) = - x - y\) với \(\left( {x;y} \right)\) thỏa mãn hệ trên.
Hướng dẫn giải
Thảo luận (1)
Bước 1: Vẽ đường thẳng \(d_1: y-2x=2\) đi qua (0;2) và (-1;0).
Lấy điểm O(0;0) không thuộc \(d_1\). Vì 0-2.0=0<2 nên O thuộc miền nghiệm
Miền nghiệm của BPT \(y - 2x \le 2\) là nửa mp bờ \(d_1\), chứa điểm O.
Bước 2: Vẽ đường thẳng \(d_2: y=4\) đi qua (0;4) và (1;4).
Lấy điểm O(0;0) không thuộc \(d_2\). Vì 0<4 nên O thuộc miền nghiệm.
Miền nghiệm của BPT \(y \le 4\) là nửa mp bờ \(d_2\), chứa điểm O.
Bước 3: Vẽ đường thẳng \(d_3: x=5\) đi qua (5;0) và (5;1).
Lấy điểm O(0;0) không thuộc \(d_3\). Vì 0<5 nên O thuộc miền nghiệm
Miền nghiệm của BPT \(x \le 5\) là nửa mp bờ \(d_3\), chứa điểm O.
Bước 4: Vẽ đường thẳng \(d_4: x + y = - 1\) đi qua (-1;0) và (0;-1).
Lấy điểm O(0;0) không thuộc \(d_4\). Vì 0+0=0>-1 nên O thuộc miền nghiệm.
Miền nghiệm của BPT \(x + y \ge - 1\) là nửa mp bờ \(d_4\), chứa điểm O.
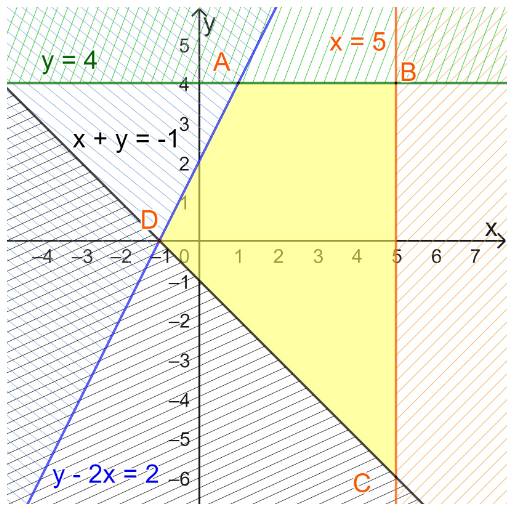
Miền biểu diễn nghiệm của hệ bất phương trình là miền tứ giác ABCD với
A(1;4); B(5;4), C(5;-6); D(-1;0).
Giá trị F tại các điểm A, B, C, D lần lượt là:
\(F\left( {1;4} \right) = - 1 - 4 = - 5\)
\(F\left( {5;4} \right) = - 5 - 4 = - 9\)
\(F\left( {5;-6} \right) = - 5 - (-6) = 1\)
\(F\left( { - 1;0} \right) = - \left( { - 1} \right) - 0 = 1\)
Vậy giá trị lớn nhất của biểu thức F(x;y) là 1 và giá trị nhỏ nhất của biểu thức F(x;y) là -9.
Trả lời bởi Hà Quang Minh
QL
Biểu diễn miền nghiệm của bất phương trình \(\dfrac{{x + y}}{2} \ge \dfrac{{2x - y + 1}}{3}\) trên mặt phẳng tọa độ.
Hướng dẫn giải
Thảo luận (1)
\(\begin{array}{l}\dfrac{{x + y}}{2} \ge \dfrac{{2x - y + 1}}{3}\\ \Leftrightarrow 3\left( {x + y} \right) \ge 2\left( {2x - y + 1} \right)\\ \Leftrightarrow 3x + 3y \ge 4x - 2y + 2\\ \Leftrightarrow x - 5y \le - 2\end{array}\)
Biểu diễn miền nghiệm của bất phương trình:
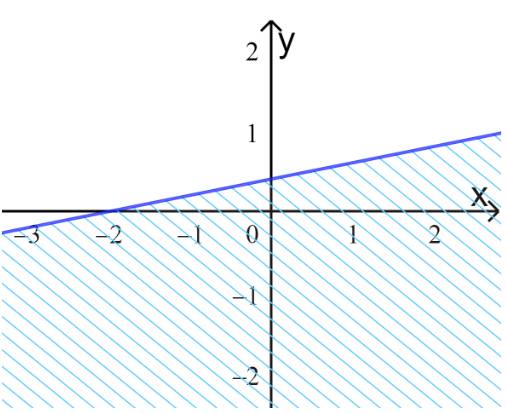
Bước 1: Vẽ đường thẳng d:\(x - 5y = - 2\) (nét liền) đi qua A(-2;0) và B(0;0,4)
Bước 2: Lấy tọa độ điểm O(0;0) thay vào biểu thức x-5y ta được: x-5y=0-5.0=0>-2
=> Điểm O không thuộc miền nghiệm của bất phương trình.
Vậy miền nghiệm của BPT đã cho là nửa mặt phẳng có bờ là đường thẳng d:\(x - 5y = - 2\) và không chứa gốc tọa độ O.
Trả lời bởi Hà Quang Minh
QL
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
A. \(\left\{ \begin{array}{l}x - y < 0\\2y \ge 0\end{array} \right.\)
B. \(\left\{ \begin{array}{l}3x + {y^3} < 0\\x + y > 3\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x + 2y < 0\\{y^2} + 3 < 0\end{array} \right.\)
D. \(\left\{ \begin{array}{l} - {x^3} + y < 4\\x + 2y < 1\end{array} \right.\)
Hướng dẫn giải
Thảo luận (1)
Ta thấy hệ \(\left\{ \begin{array}{l}x - y < 0\\2y \ge 0\end{array} \right.\) là hệ bất phương trình bậc nhất hai ẩn với các bất phương trình bậc nhất hai ẩn là \(x - y < 0;2y \ge 0\).
=> Chọn A.
Đáp án B loại vì \(3x + {y^3} < 0\) chứa \(y^3\).
Đáp án C loại vì \({y^2} + 3 < 0\) chứa \(y^2\).
Đáp án D loại vì \( - {x^3} + y < 4\) chứa \(x^3\).
Trả lời bởi Hà Quang Minh
QL
Cho bất phương trình 2x+y>3. Khẳng định nào sau đây là đúng?
A. Bất phương trình đã cho có nghiệm duy nhất
B. Bất phương trình đã cho vô nghiệm
C. Bất phương trình đã cho có vô số nghiệm
D. Bất phương trình đã cho có tập nghiệm là \(\left[ {3; + \infty } \right)\)
Hướng dẫn giải
Thảo luận (1)
Bất phương trình 2x+y > 3 là bất phương trình bậc nhất hai ẩn và có vô số nghiệm.
Chọn C.
Trả lời bởi Hà Quang Minh
QL
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
A. \(x + y > 3\)
B. \({x^2} + {y^2} \le 4\)
C. \(\left( {x - y} \right)\left( {3x + y} \right) \ge 1\)
D. \({y^3} - 2 \le 0\)
Hướng dẫn giải
Thảo luận (2)
Đáp án A: \(x + y > 3\) là bất phương trình bậc nhất hai ẩn x và y có a=1, b=1, c=3
Đáp án B: \({x^2} + {y^2} \le 4\) không là bất phương trình bậc nhất hai ẩn vì có \({x^2},{y^2}\)
Đáp án C: \(\left( {x - y} \right)\left( {3x + y} \right) \ge 1 \Leftrightarrow 3{x^2} - 2xy - {y^2} \ge 1\) không là bất phương trình bậc nhất hai ẩn vì có \({x^2},{y^2}\)
Đáp án D: \({y^3} - 2 \le 0\) không là bất phương trình bậc nhất hai ẩn vì có \({y^3}\).
Chọn A
Trả lời bởi Hà Quang Minh
QL
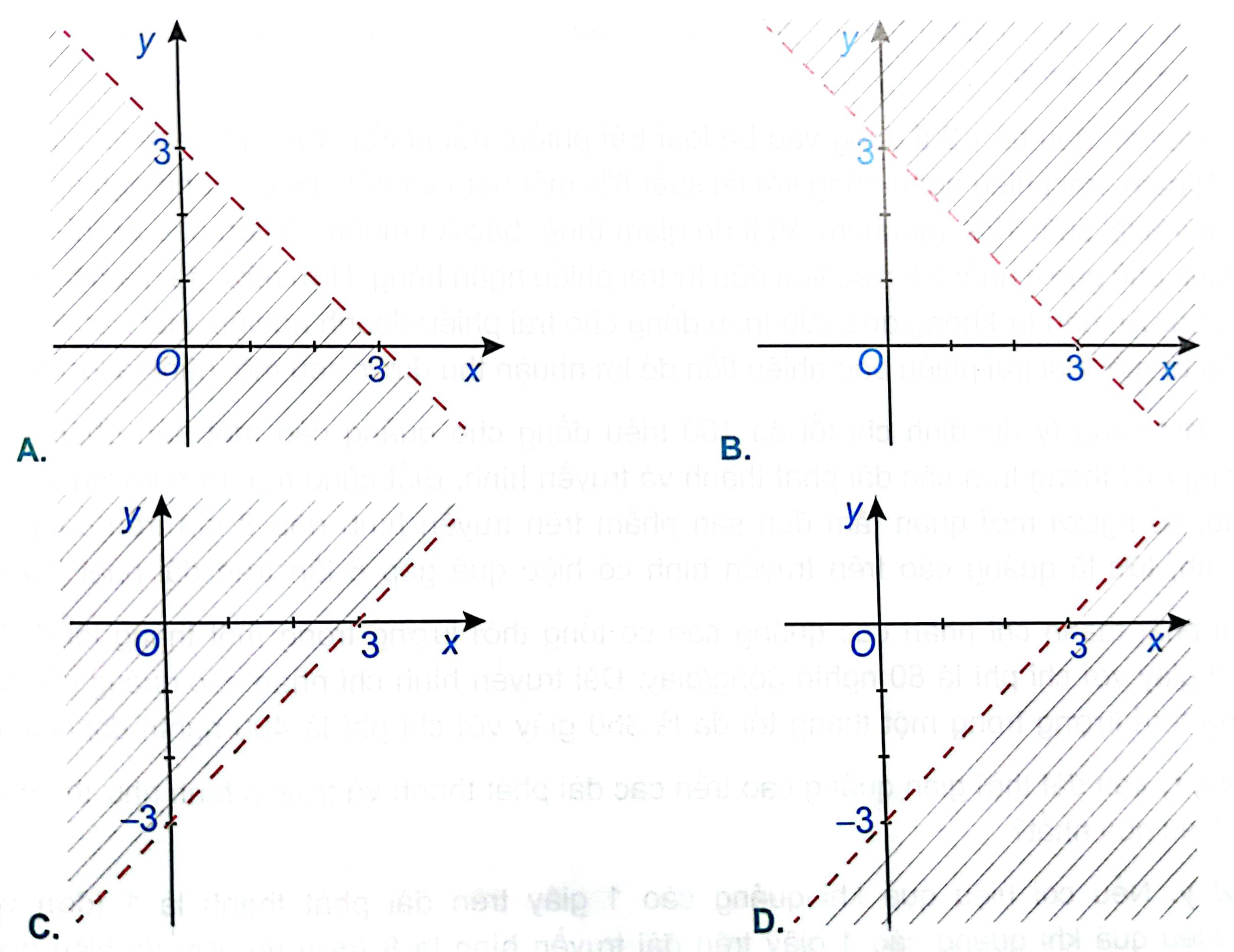
Hình nào sau đây biểu diễn miền nghiệm của bất phương trình \(x - y < 3\)?
Hướng dẫn giải
Thảo luận (1)
Đường thẳng x-y=3 đi qua điểm A(0;-3)
=> Loại đáp án A, B vì hai đường thẳng trong hình không đi qua A.
Xét điểm O(0;0) ta có: 0-0=0 < 3
=> Điểm O thuộc miền nghiệm của bất phương trình x-y<3
Chọn D
Trả lời bởi Hà Quang Minh
QL
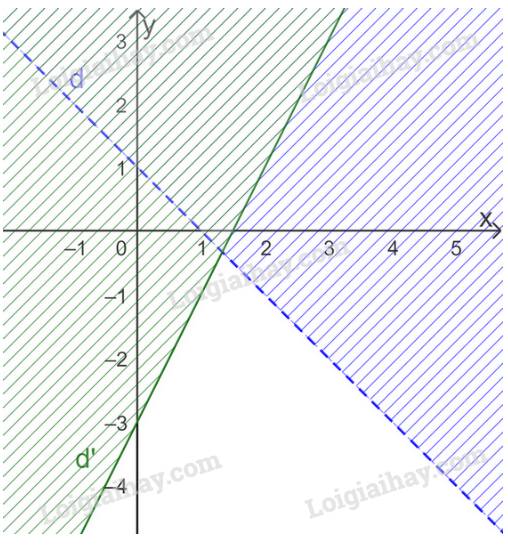
Biểu diễn miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x + y < 1\\2x - y \ge 3\end{array} \right.\) trên mặt phẳng tọa độ.
Hướng dẫn giải
Thảo luận (1)
Tham khảo:
Xác định miền nghiệm của bất phương trình \(x + y < 1\)
+ Vẽ đường thẳng d: x+y=1 (nét đứt) đi qua (0;1) và (1;0)
+ Vì 0+0=0 < 1 nên điểm O(0;0) thuộc miền nghiệm của bpt
Do đó, miền nghiệm của bất phương trình \(x + y < 1\) là nửa mặt phẳng bờ d chứa gốc tọa độ O.
Xác định miền nghiệm của bất phương trình \(2x - y \ge 3\)
+ Vẽ đường thẳng d’: \(2x - y = 3\) đi qua (1;-1) và (0;-3)
+ Vì 2.0-0=0
Do đó, miền nghiệm của bất phương trình \(2x - y \ge 3\) là nửa mặt phẳng bờ d’ không chứa gốc tọa độ O.
Vậy miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho (Không đường thẳng d’).
Cách 1:
Gọi x là số tiền mua trái phiếu chính phủ và y là số tiền mua trái phiếu ngân hàng. (đơn vị triệu đồng) (\(x,y \le 1200\))
Khi đó, số tiền mua trái phiếu doanh nghiệp là \(1200 - x - y\)(triệu đồng)
Vì số tiền đầu tư trái phiếu chính phủ gấp ít nhất 3 lần số tiền đầu tư trái phiếu ngân hàng nên \(x \ge 3y\)
Vì bác An đầu tư không quá 200 triệu đồng cho trái phiếu doanh nghiệp nên \(1200 - x - y \le 200 \Leftrightarrow x + y \ge 1000\)
Từ điều kiện của bài toán ta có số tiền bác An đầu tư trái phiếu phải thỏa mãn hệ:
\(\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 1200}\\{0 \le y \le 1200}\\{x + y \ge 1000}\\{x - 3y \ge 0}\end{array}} \right.\)
Biểu diễn miền nghiệm của hệ trong mp tọa độ ta được
Miền nghiệm là miền tứ giác ABCD với: A(750;250); B(1000;0); C(1200;0); D(1200;400)
Lợi nhuận thu được sau một năm là
\(\begin{array}{*{20}{l}}{F\left( {x;y} \right) = x.7\% \; + y.8\% \; + (1200 - x - y).12\% }\\{ = 144 - 0,05x - 0,04y}\end{array}\)
Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 1200}\\{0 \le y \le 1200}\\{x + y \ge 1000}\\{x - 3y \ge 0}\end{array}} \right.\)
Thay tọa độ các điểm A, B vào biểu thức F(x;y) ta được:
\(F\left( {750;250} \right) = 144 - 0,05.750 - 0,04.250 = 96,5\)
\(F\left( {1000;0} \right) = 144 - 0,05.1000 - 0,04.0 = 94\)
\(F\left( {1200;0} \right) = 144 - 0,05.1200 - 0,04.0 = 84\)
\(F\left( {1200;400} \right) = 144 - 0,05.1200 - 0,04.400 = 68\)
=> F đạt giá trị lớn nhất là 96,5 nếu x=750 và y=250.
Vậy bác An nên đầu tư 750 trái phiếu chính phủ; 250 triệu đồng trái phiếu ngân hàng và 200 triệu trái phiếu doanh nghiệp.
Trả lời bởi Hà Quang Minh