Bài tập cuối chương I

a) \(\{ a\}  \in \{ a;b;c;d\} \) là mệnh đề sai, vì không có quan hệ \( \in \) giữa hai tập hợp.

b) \(\emptyset  = \{ 0\} \) là mệnh đề sai, vì tập rỗng là tập không có phần tử nào, còn tập {0} có một phần tử là 0.

c) \(\{ a;b;c;d\}  = \{ b;a;d;c\} \) là mệnh đề đúng (có thể thay đổi tùy ý vị trí các phần tử trong một tập hợp).

d) \(\{ a;b;c\}  \not {\subset} \{ a;b;c\} \) là mệnh đề sai, vì mỗi phần tử a,b,c đều thuộc tập hợp \(\{ a;b;c\} \).

a) Mệnh đề có dạng \(P \Rightarrow Q\) với P: “\(2a - 1 > 0\)” và Q: “\(a > 0\)”

Ta thấy khi P đúng (tức là \(a > \frac{1}{2}\)) thì Q cũng đúng. Do đó, \(P \Rightarrow Q\) đúng.

b) Mệnh đề có dạng \(P \Leftrightarrow Q\) với P: “\(a - 2 > b\)” và Q: “\(a > b + 2\)”

Khi P đúng thì Q cũng đúng, do đó, \(P \Rightarrow Q\) đúng.

Khi Q đúng thì P cũng đúng, do đó, \(Q \Rightarrow P\) đúng.

Vậy mệnh đề \(P \Leftrightarrow Q\) đúng.

a) Mệnh đề trên có dạng “Nếu P thì Q” là mệnh đề kéo theo \(P \Rightarrow Q\), với:

P: “\(B \subset A\)” và Q: “\(A \cup B = A\)”. Có thể phát biểu dưới dạng:

\(B \subset A\) là điều kiện đủ để có \(A \cup B = A\)

\(A \cup B = A\) là điều kiện cần để có \(B \subset A\)

b) Mệnh đề trên có dạng “Nếu P thì Q” là mệnh đề kéo theo \(P \Rightarrow Q\), với:

P: “Hình bình hành ABCD có hai đường chéo vuông góc với nhau” và Q: “ABCD là hình thoi”. Có thể phát biểu dưới dạng:

Hình bình hành ABCD có hai đường chéo vuông góc với nhau là điều kiện đủ để ABCD là hình thoi.

ABCD là hình thoi là điều kiện cần để có ABCD là hình bình hành có hai đường chéo vuông góc với nhau.

Mệnh đề trên có dạng “P nếu và chỉ nếu Q”, là một mệnh đề tương đương với P: “\(x \in \mathbb{Z}\)” và Q: “\(x + 1 \in \mathbb{Z}\)” (\(x \in \mathbb{R}\))

Phát biểu:

 “\(\forall x \in \mathbb{R},x \in \mathbb{Z}\) là điều kiện cần và đủ để có \(x + 1 \in \mathbb{Z}\)”

Hoặc “\(\forall x \in \mathbb{R},x + 1 \in \mathbb{Z}\) là điều kiện cần và đủ để có \(x \in \mathbb{Z}\)”

a) Mệnh đề “\(\forall x \in \mathbb{N},{x^3} > x\)” sai vì \(0 \in \mathbb{N}\) nhưng \({0^3} = 0.\)

b) Mệnh đề “\(\exists x \in \mathbb{Z},x \notin \mathbb{N}\)” đúng, chẳng hạn \( - 2 \in \mathbb{Z}, - 2 \notin \mathbb{N}.\)

c) Mệnh đề “\(\forall x \in \mathbb{R},\) nếu \(x \in \mathbb{Z}\) thì \(x \in \mathbb{Q}\)” đúng vì \(\mathbb{Z} \subset \mathbb{Q}.\)

Tham khảo:

Ta có:

Mỗi hình chữ nhật là một hình bình hành đặc biệt (có một góc vuông). Do đó: \(C \subset B\)

Mỗi hình thoi là một hình bình hành đặc biệt (có hai cạnh kề bằng nhau). Do đó: \(E \subset B\)

Mỗi hình bình hành là một hình tứ giác (có một cặp cạnh đối song song và bằng nhau). Do đó: \(B \subset A\)

\(C \cap E\)là tập hợp các hình vừa là hình chữ nhật vừa là hình thoi, hay là hình chữ nhật có 4 cạnh bằng nhau (hình vuông). Do đó: \(C \cap E = D\)

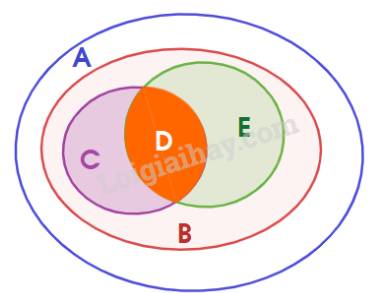
Kết hợp lại ta có: \(\left\{ \begin{array}{l}D \subset C \subset B \subset A,\\D \subset E \subset B \subset A,\\C \cap E = D\end{array} \right.\)

Biểu đồ Ven:

a) Các tập hợp con của tập hợp \(A = \{ a;b;c\} \)gồm:

+) Tập rỗng: \(\emptyset \)

+) Tập con có 1 phần tử: \(\{ a\} ,\{ b\} ,\{ c\} .\)

+) Tập con có 2 phần tử: \(\{ a;b\} ,\{ b;c\} ,\{ c;a\} .\)

+) Tập hợp A.

b) Tập hợp B thỏa mãn \(\{ a;b\}  \subset B \subset \{ a;b;c;d\} \)là:

+) \(B = \{ a;b\} \)

+) \(B = \{ a;b;c\} \)

+) \(B = \{ a;b;d\} \)

+) \(B = \{ a;b;c;d\} \)

Chú ý

Mọi tập hợp A luôn có hai tập con là \(\emptyset \) và A.

Phương trình \({x^2} - 5x - 6 = 0\) có hai nghiệm là -1 và 6, nên \(A = \{  - 1;6\} \)

Phương trình \({x^2} = 1\) có hai nghiệm là 1 và -1, nên \(B = \{  - 1;1\} \)

Do đó

\(\begin{array}{l}A \cap B = \{  - 1\} ,\\A \cup B = \{  - 1;1;6\} ,\\A\backslash B = \{ 6\} ,\\B\backslash A = \{ 1\} ,\end{array}\)

Tham khảo:

Ta có:

Bất phương trình \(1 - 2x \le 0\) có nghiệm là \(x \ge \frac{1}{2}\) hay \(A = [\frac{1}{2};+\infty)\)

Bất phương trình \(x - 2 < 0\) có nghiệm là \(x < 2\) hay \(B = ( - \infty ;2)\)

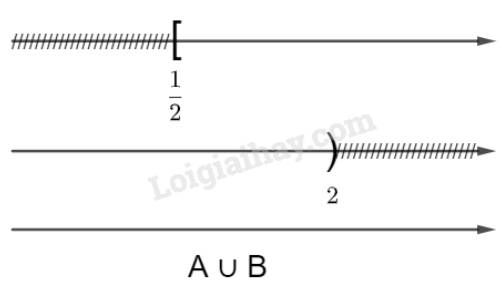
Vậy \(A \cup B = \mathbb R\)

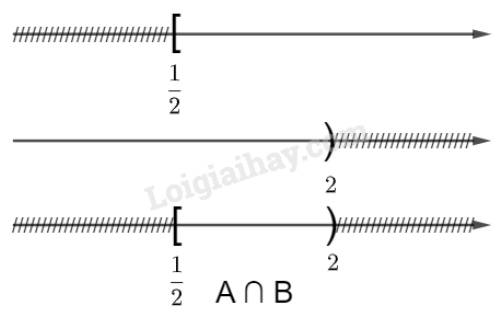
Vậy \(A \cap B = [\frac{1}{2};2)\)

Tham khảo:

Gọi X là tập hợp các học sinh của lớp 10C.

A là tập hợp các học sinh tham gia cuộc thi vẽ đồ họa trên máy tính,

B là tập hợp các học sinh tham gia cuộc thi tin học văn phòng cấp trường.

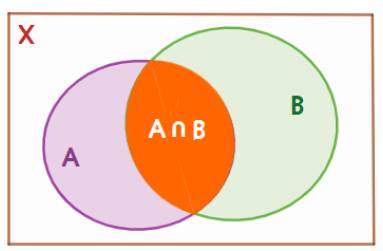
Theo biểu đồ Ven ta có: \(n(A) = 18,\;n(B) = 24,\;n(X) = 45.\)

\(n(A \cup B)\) là số học sinh tham gia ít nhất một trong hai cuộc thi, bằng: 45 -9 = 36 (học sinh)

Mà \(n(A \cup B) = n(A) + n(B) - n(A \cap B)\) (do các học sinh tham gia cả 2 cuộc thi được tính hai lần)

Suy ra số học sinh tham gia cả 2 cuộc thi là: \(n(A \cap B) = 18 + 24 - 36 = 6\)

Vậy có 6 học sinh của lớp 10C tham gia đồng thời hai cuộc thi.