Hình 28 mô tả một đĩa tròn bằng bìa cứng được chia làm 6 phần bằng nhau và ghi các số 1, 2, 3, 4, 5, 6; chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn và ghi lại số ở hình quạt mà chiếc kim chỉ vào khi đĩa dừng lại. mẫu số liệu dưới đây ghi lại số liệu sau 40 lần quay đĩa tròn:a) Trong 40 số liệu thống kê ở trên, có bao nhiêu giá trị khác nhau?b) Tìm tần số của mỗi giá trị đó.Lập bảng tần số của mẫu số liệu thống kê đó.Vẽ biểu đồ tần số ở dạng biểu đồ cột của mẫu số...
Đọc tiếp
Hình 28 mô tả một đĩa tròn bằng bìa cứng được chia làm 6 phần bằng nhau và ghi các số 1, 2, 3, 4, 5, 6; chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn và ghi lại số ở hình quạt mà chiếc kim chỉ vào khi đĩa dừng lại. mẫu số liệu dưới đây ghi lại số liệu sau 40 lần quay đĩa tròn:


a) Trong 40 số liệu thống kê ở trên, có bao nhiêu giá trị khác nhau?
b) Tìm tần số của mỗi giá trị đó.
Lập bảng tần số của mẫu số liệu thống kê đó.
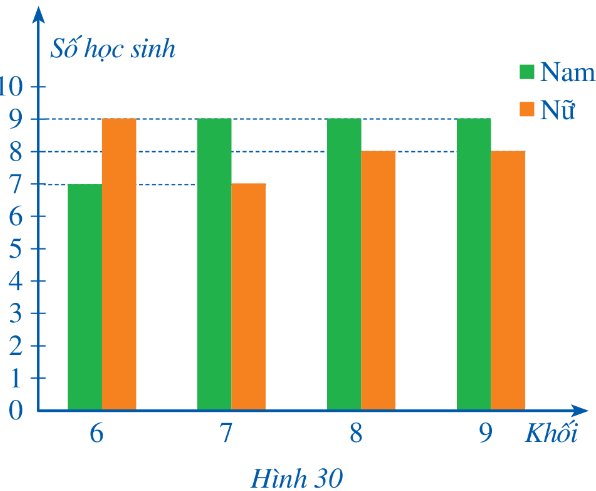
Vẽ biểu đồ tần số ở dạng biểu đồ cột của mẫu số liệu thống kê đó.
c) Tìm tần số tương đối của mỗi giá trị đó.
Lập bảng tần số tương đối của mẫu số liệu thống kê đó.
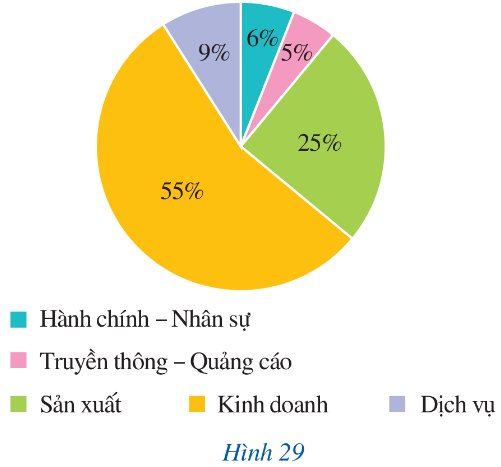
Vẽ biểu đồ tần số tương đối ở dạng biểu đồ cột và biểu đồ hình quạt tròn của mẫu số liệu thống kê đó.
















a) Tần số ghép nhóm của [70; 80) là 23, chọn đáp án D.
b) Tần số ghép nhóm của [50; 60) là 4.
Tần số tương đối ghép nhóm của [50; 60) là \(\frac{4}{{40}}.100\% = 10\% \). Chọn đáp án A.
Trả lời bởi datcoder