Bài tập cuối chương 4

Đáp án đúng là: B

Vì H, K lần lượt là trung điểm của AC, BC nên HK là đường trung bình của tam giác ABC suy ra \(HK = \dfrac{1}{2}AB\)

Do đó AB = 2HK = 2 . 3,5 = 7 (cm).

Vậy AB = 7 cm.

Xét tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC

⇒ MN, NP, PM là đường trung bình của tam giác ABC

\(\Rightarrow\left\{{}\begin{matrix}MN=\dfrac{1}{2}BC\\NP=\dfrac{1}{2}AB\\PM=\dfrac{1}{2}AC\end{matrix}\right.\)

Khi đó chu vi tam giác MNP là

P = MN + NP + PM = \(\dfrac{1}{2}\left(AB+AC+BC\right)=\dfrac{1}{2}.P_{ABC}=\dfrac{1}{2}\cdot32=16\left(cm\right)\)

Đáp án đúng là: C

Vì tam giác ABC cân tại A nên AB = AC = 15 cm.

Theo đề bài, BD là tia phân giác của \(\widehat {ABC}\), áp dụng tính chất đường phân giác vào tam giác ABC, ta có:

\(\dfrac{{AB}}{{BC}} = \dfrac{{A{\rm{D}}}}{{C{\rm{D}}}} = \dfrac{{15}}{{10}} = \dfrac{3}{2}\) suy ra \(\dfrac{{A{\rm{D}}}}{3} = \dfrac{{C{\rm{D}}}}{2}\)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\dfrac{{A{\rm{D}}}}{3} = \dfrac{{C{\rm{D}}}}{2} = \dfrac{{A{\rm{D}} + C{\rm{D}}}}{{3 + 2}} = \dfrac{{AC}}{5} = \dfrac{{15}}{5} = 3\)

Do đó AD = 3 . 3 = 9 (cm).

Vậy AD = 9 cm.

Từ điểm B kẻ đường thẳng song song với AC cắt Oy tại D hay AC // BD.

Áp dụng định lí Thalès vào tam giác OBD, ta có:

\(\dfrac{{OA}}{{OB}} = \dfrac{{OC}}{{O{\rm{D}}}}\) hay \(\dfrac{2}{5} = \dfrac{3}{{O{\rm{D}}}}\)

Suy ra: \(O{\rm{D}} = \dfrac{{5.3}}{2} = 7,5(cm)\)

Ta có OD = OC + CD suy ra CD = OD – OC = 7,5 – 3 = 4,5 (cm).

Vậy CD = 4,5 cm.

Cách 1.

a) Theo đề bài, tam giác ABC vuông tại A nên \(\widehat {BAC} = {90^o}\) hay AB ⊥ AC.

Vì D, E lần lượt là trung điểm của AB, BC nên DE là đường trung bình của tam giác ABC suy ra DE // AC.

Mà AB ⊥ AC nên AB ⊥ DE hay \(\widehat {A{\rm{D}}E} = {90^o}\).

Tương tự, ta chứng minh được: EF ⊥ AC hay \(\widehat {AEF} = {90^o}\)

Ta có: \(\widehat {BAC} + \widehat {A{\rm{D}}E} + \widehat {AFE} + \widehat {DEF} = {360^o}\)

90°+90°+90^o\( + \widehat {DEF}\) = 360^o
270°+ \(\widehat {DEF}\)=360°

Suy ra \(\widehat {DEF}\)=360°−270°=90^o

Tứ giác ADEF có \(\widehat {BAC} = {90^o};\widehat {A{\rm{D}}E} = {90^o};\widehat {AEF} = {90^o};\widehat {DEF} = {90^{^o}}\)

Do đó tứ giác ADEF là hình chữ nhật.

Suy ra hai đường chéo AE và DF bằng nhau.

Vậy AE = DF (đpcm).

b) Vì D, F lần lượt là trung điểm của AB, AC nên DF là đường trung bình của tam giác ABC.

Suy ra DF // BC hay DF // BE.

Vì tứ giác ADEF là hình chữ nhật nên AD // EF hay BD // EF.

Tứ giác BDFE có DF // BE và BD // EF nên tứ giác BDFE là hình bình hành.

Hình bình hành BDFE có hai đường chéo BF và DE.

Mà I là trung điểm của DE nên I cũng là trung điểm của BF.

Do đó, ba điểm B, I, F thẳng hàng.

Vì BD và CE là đường trung tuyến nên E, D lần lượt là trung điểm của AB, AC.

Suy ra DE là đường trung bình của tam giác ABC.

Khi đó, DE // BC và \(DE = \dfrac{1}{2}BC\)       (1)

Vì I, K lần lượt là trung điểm của GB, GC nên IK là đường trung bình của tam giác GBC suy ra IK // BC và \(IK = \dfrac{1}{2}BC\) (2)

Từ (1) và (2) suy ra DE // IK và \(DE = IK = \dfrac{1}{2}BC\)

Tứ giác EDKI có DE // IK và DE = IK nên tứ giác EDKI là hình bình hành (đpcm).

Áp dụng định lí Thalès:

• Vì IM // BK nên \(\dfrac{{AI}}{{AB}} = \dfrac{{AM}}{{AK}}\)suy ra AB . AM = AI . AK           (1)

• Vì KN // IC nên \(\dfrac{{AN}}{{AI}} = \dfrac{{AK}}{{AC}}\) suy ra AN . AC = AI . AK            (2)

Từ (1) và (2) suy ra AB . AM = AN . AC = AI . AK        

Do đó \(\dfrac{{AN}}{{AB}} = \dfrac{{AM}}{{AC}}\) (theo tính chất tỉ lệ thức).

Suy ra MN // BC (theo định lí Thalès đảo).

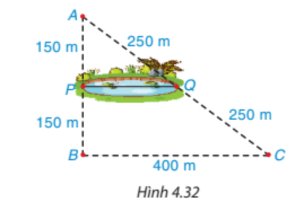
Áp dụng định lí Ta-lét trong tam giác ABC có PQ // BC, ta có:

\(\dfrac{PQ}{BC}=\dfrac{AP}{AB}=\dfrac{AP}{AP+PB}\\ \Leftrightarrow\dfrac{PQ}{400}=\dfrac{150}{150+150}\\ \Leftrightarrow PQ=200\left(m\right).\)