Tính:
a) \(({x^2} - 6)({x^2} + 6)\);
b) \((x - 1)({x^2} + x + 1)\).
Tính:
a) \(({x^2} - 6)({x^2} + 6)\);
b) \((x - 1)({x^2} + x + 1)\).
Tính:
a) \(\dfrac{1}{2}{x^2}.\dfrac{6}{5}{x^3}\); b) \({y^2}(\dfrac{5}{7}{y^3} - 2{y^2} + 0,25)\);
c) \((2{x^2} + x + 4)({x^2} - x - 1)\); d) \((3x - 4)(2x + 1) - (x - 2)(6x + 3)\).
a)
\(\dfrac{1}{2}{x^2}.\dfrac{6}{5}{x^3} = \dfrac{1}{2}.\dfrac{6}{5}.{x^2}.{x^3} = \dfrac{3}{5}{x^5}\);
b)
\(\begin{array}{l}{y^2}(\dfrac{5}{7}{y^3} - 2{y^2} + 0,25) = {y^2}.\dfrac{5}{7}{y^3} - {y^2}.2{y^2} + {y^2}.0,25)\\ = \dfrac{5}{7}{y^5} - 2{y^4} + 0,25{y^2}\end{array}\);
c)
\(\begin{array}{l}(2{x^2} + x + 4)({x^2} - x - 1) \\= 2{x^2}({x^2} - x - 1) + x({x^2} - x - 1) + 4({x^2} - x - 1)\\ = 2{x^4} - 2{x^3} - 2{x^2} + {x^3} - {x^2} - x + 4{x^2} - 4x - 4 \\= 2{x^4} - {x^3} + {x^2} - 5x - 4\end{array}\);
d)
\(\begin{array}{l}(3x - 4)(2x + 1) - (x - 2)(6x + 3) \\= 3x(2x + 1) - 4(2x + 1) - x(6x + 3) + 2(6x + 3)\\ = 6{x^2} + 3x - 8x - 4 - 6{x^2} - 3x + 12x + 6\\ = 4x + 2\end{array}\).
Trả lời bởi Hà Quang MinhCho đơn thức \(P(x) = 2x\) và đa thức \(Q(x) = 3{x^2} + 4x + 1\).
a) Hãy nhân đơn thức P(x) với từng đơn thức của đa thức Q(x).
b) Hãy cộng các tích vừa tìm được.
a)
Các đơn thức của đa thức Q(x) là: \(3{x^2};4x;1\).
Tích của đơn thức P(x) với từng đơn thức của đa thức Q(x) lần lượt là: \(2x.3{x^2} = 6{x^3};2x.4x = 8{x^2};2x.1 = 2x\).
b) Cộng các tích vừa tìm được:
\(6{x^3} + 8{x^2} + 2x\).
Trả lời bởi Hà Quang MinhCho đa thức \(P(x) = 2x + 3\) và đa thức \(Q(x) = x + 1\).
a) Hãy nhân mỗi đơn thức của đa thức P(x) với từng đơn thức của đa thức Q(x).
b) Hãy cộng các tích vừa tìm được.
a)
Các đơn thức của đa thức P(x) là: \(2x;3\).
Các đơn thức của đa thức Q(x) là: \(x;1\).
Tích mỗi đơn thức P(x) với từng đơn thức của đa thức Q(x) lần lượt là: \(2{x^2};2x;3x;3\).
b) Cộng các tích vừa tìm được:
\(2{x^2} + 2x + 3x + 3 = 2{x^2} + 5x + 3\).
Trả lời bởi Hà Quang MinhTính:
a) \(\dfrac{1}{2}x(6x - 4)\);
b) \( - {x^2}(\dfrac{1}{3}{x^2} - x - \dfrac{1}{4})\).
a) \(\dfrac{1}{2}x(6x - 4) = \dfrac{1}{2}x.6x + \dfrac{1}{2}x.( - 4) = 3{x^2} - 2x\).
b) \(\begin{array}{l} - {x^2}(\dfrac{1}{3}{x^2} - x - \dfrac{1}{4}) = - {x^2}.\dfrac{1}{3}{x^2} + - {x^2}. - x + - {x^2}. - \dfrac{1}{4}\\ = - \dfrac{1}{3}{x^4} + {x^3} + \dfrac{1}{4}{x^2}\end{array}\)
Trả lời bởi Hà Quang MinhQuan sát hình chữ nhật MNPQ ở Hình 3.
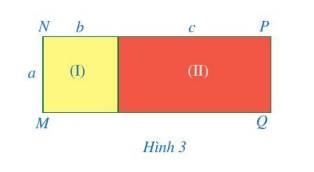
a) Tính diện tích mỗi hình chữ nhật (I), (II);
b) Tính diện tích của hình chữ nhật MNPQ;
c) So sánh: \(a(b + c)\) và \(ab + ac\).
a)
Diện tích của hình chữ nhật (I) là: \(a.b\).
Diện tích của hình chữ nhật (II) là: \(a.c\).
b) Diện tích của hình chữ nhật MNPQ là: \(ab + ac\).
c) Ta có: \(a(b + c) = a.b + a.c\).
Vậy \(a(b + c)\) = \(ab + ac\).
Trả lời bởi Hà Quang MinhThực hiện phép tính:
a) \({x^2}.{x^4}\); b) \(3{x^2}.{x^3}\); c) \(a{x^m}.b{x^n}\) (a ≠ 0; b ≠ 0; m, n \(\in\) N).
a) \({x^2}.{x^4} = {x^{2 + 4}} = {x^6}\).
b) \(3{x^2}.{x^3} = 3.1.{x^{2 + 3}} = 3{x^5}\).
c) \(a{x^m}.b{x^n} = a.b.{x^{m + n}}\) (a ≠ 0; b ≠ 0; m, n \(\in\) N).
Trả lời bởi Hà Quang MinhTrong quá trình biến đổi và tính toán những biểu thức đại số, nhiều khi ta phải thực hiện phép nhân hai đa thức một biến, chẳng hạn ta cần thực hiện phép nhân sau:
\((x - 1)({x^2} + x + 1)\)
Làm thế nào để thực hiện được phép nhân hai đa thức một biến?
Muốn nhân một đa thức với một đa thức, ta nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia rồi cộng các tích với nhau.
Trả lời bởi Hà Quang MinhTính:
a) \(3{x^5}.5{x^8}\);
b) \( - 2{x^{m + 2}}.4{x^{n - 2}}\) (m, n \(\in\) N; n > 2).
a) \(3{x^5}.5{x^8} = 3.5.{x^5}.{x^8} = 15.{x^{5 + 8}} = 15.{x^{13}}\).
b) \( - 2{x^{m + 2}}.4{x^{n - 2}} = - 2.4.{x^{m + 2}}.{x^{n - 2}} = - 8.{x^{m + 2 + n - 2}} = - 8.{x^{m + n}}\) (m, n \(\in\) N; n > 2).
Trả lời bởi Hà Quang MinhQuan sát hình chữ nhật MNPQ ở Hình 4.
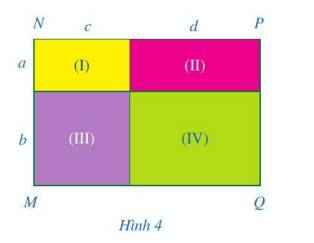
a) Tính diện tích mỗi hình chữ nhật (I), (II), (III), (IV).
b) Tính diện tích của hình chữ nhật MNPQ.
c) So sánh: \((a + b)(c + d)\) và \(ac + ad + bc + bd\).
a)
Diện tích của hình chữ nhật (I) là: \(a.c\).
Diện tích của hình chữ nhật (II) là: \(a.d\).
Diện tích của hình chữ nhật (III) là: \(b.c\).
Diện tích của hình chữ nhật (IV) là: \(b.d\).
b) Diện tích hình chữ nhật MNPQ là: \(ac + ad + bc + bd\).
c) Ta có:
\((a + b)(c + d) = a(c + d) + b(c + d) = ac + ad + bc + bd\).
Vậy \((a + b)(c + d)\) = \(ac + ad + bc + bd\).
Trả lời bởi Hà Quang Minh
a) \(\begin{array}{l}({x^2} - 6)({x^2} + 6) = {x^2}({x^2} + 6) + ( - 6).({x^2} + 6) = {x^2}.{x^2} + {x^2}.6) + ( - 6).{x^2} + ( - 6).6\\ = {x^4} + 6{x^2} - 6{x^2} - 36 = {x^4} - 36\end{array}\)
b) \(\begin{array}{l}(x - 1)({x^2} + x + 1) = x({x^2} + x + 1) + ( - 1)({x^2} + x + 1) = x.{x^2} + x.x + x.1 + ( - 1).{x^2} + ( - 1).x + ( - 1).1\\ = {x^3} + {x^2} + x - {x^2} - x - 1 = {x^3} - 1\end{array}\)
Trả lời bởi Hà Quang Minh