Cho tam giác ABC trong Hình 1.
- Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ dài của ba cạnh a,b,c
- Hãy sắp xếp theo thứ tự từ nhỏ đến lớn độ lớn độ lớn của ba góc A,B,C là các góc đối diện với ba cạnh a,b,c.
- Nêu nhận xét của em về hai kết quả sắp xếp trên.
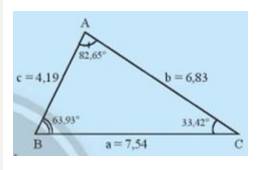
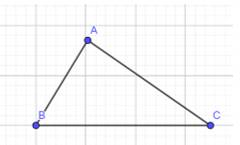
- Độ dài các cạnh từ nhỏ đến lớn là c, b, a
- Các góc từ nhỏ đến lớn là C, B, A
- Ta thấy trong tam giác ABC cạnh đối diện với góc lớn hơn thì lớn hơn và ngược lại.
Trả lời bởi Hà Quang Minh