Câu khẳng định có dạng “ Nếu … thì…” trong toán học được gọi là gì?
Bài 4. Định lí
QL
Hướng dẫn giải
Thảo luận (1)
QL
Xét khẳng định “Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau” , ta thấy: Khẳng định này được phát biểu dưới dạng “ Nếu .. thì..” Trong khẳng định đó, hãy nêu:
- Phần nằm giữa từ “ Nếu” và từ “ thì”
- Phần nằm sau từ “ thì”.
Hướng dẫn giải
Thảo luận (1)
- Phần nằm giữa từ “ Nếu” và từ “ thì” là: một đường thẳng cắt hai đường thẳng song song
- Phần nằm sau từ “ thì” là: hai góc so le trong bằng nhau
Trả lời bởi Hà Quang Minh
QL
Nêu giả thiết và kết luận của định lí: “ Nếu một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng a, b song song với nhau”.
Hướng dẫn giải
Thảo luận (1)
- Giả thiết: một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc so le trong bằng nhau
- Kết luận: hai đường thẳng a, b song song với nhau
Trả lời bởi Hà Quang Minh
QL
Cho định lí:
“ Nếu hai góc đối đỉnh thì hai góc đó bằng nhau”.
a) Vẽ hình minh họa nội dung định lí trên.
b) Viết giả thiết và kết luận của định lí trên.
c) Chứng tỏ định lí trên là đúng.
Hướng dẫn giải
Thảo luận (1)
a)
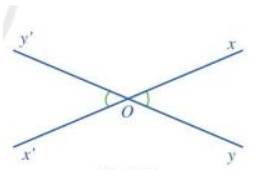
b)
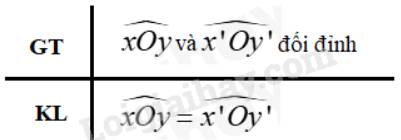
c) Vì góc xOy và x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau; Ox và Ox’ là hai tia đối nhau
\( \Rightarrow \widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù; \(\widehat {xOy'}\) và \(\widehat {x'Oy'}\) là hai góc kề bù
\( \Rightarrow \widehat {xOy} + \widehat {xOy'} = 180^\circ \); \(\widehat {xOy'} + \widehat {x'Oy'} = 180^\circ \) ( tính chất 2 góc kề bù)
\( \Rightarrow \)\(\widehat {xOy} = \widehat {x'Oy'}\) (đpcm)
Trả lời bởi Kiều Sơn Tùng
QL
Chứng minh định lí: “ Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bằng nhau”
Hướng dẫn giải
Thảo luận (1)

Ta có: \(\widehat {{A_1}} = \widehat {{B_1}}\) (gt)
\(\widehat {{A_3}} = \widehat {{A_1}}\) (2 góc đối đỉnh)
\( \Rightarrow \widehat {{A_3}} = \widehat {{B_1}}\) ( cùng bằng \(\widehat {{A_1}}\))
Mà \(\widehat {{A_2}} + \widehat {{A_3}} = 180^\circ ;\widehat {{B_1}} + \widehat {{B_4}} = 180^\circ \) ( 2 góc kề bù)
\( \Rightarrow \widehat {{A_2}} = \widehat {{B_4}}\)
Trả lời bởi Kiều Sơn Tùng
QL
Vẽ hình minh họa và viết giả thiết, kết luận bằng kí hiệu cho mỗi định lí sau:a) Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lạib) Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.c) Qua một điểm cho trước có duy nhất một đường thẳng vuông góc với đường thẳng cho trước.
Đọc tiếp
Vẽ hình minh họa và viết giả thiết, kết luận bằng kí hiệu cho mỗi định lí sau:
a) Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại
b) Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.
c) Qua một điểm cho trước có duy nhất một đường thẳng vuông góc với đường thẳng cho trước.
Hướng dẫn giải
Thảo luận (1)
QL
Cho định lí: “ Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.”
a) Vẽ hình minh họa nội dung định lí trên.
b) Viết giải thiết, kết luận của định lí trên.
c) Chứng minh định lí trên.
Hướng dẫn giải
Thảo luận (1)
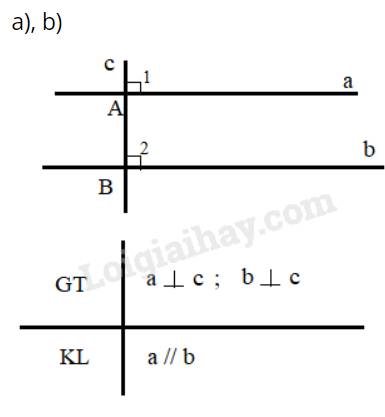
c) Giả sử có 2 đường thẳng phân biệt a,b cùng vuông góc với một đường thẳng c.
Ta có: \(\widehat {{A_1}} = \widehat {{B_2}}\), mà hai góc này ở vị trí đồng vị nên a//b (Dấu hiệu nhận biết 2 đường thẳng song song)
Như vậy, định lí trên có thể được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song.
Trả lời bởi Kiều Sơn Tùng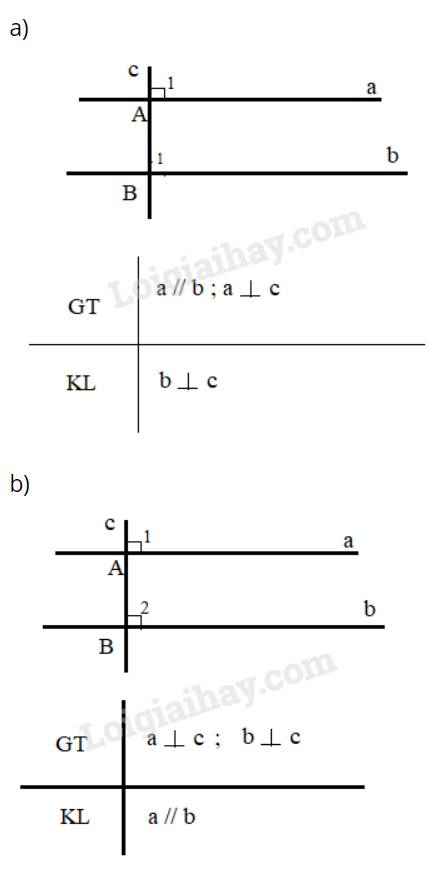

Câu khẳng định có dạng “ Nếu … thì…” trong toán học được gọi là định lí
Trả lời bởi Hà Quang Minh