Quan sát ê ke có góc 60\(^\circ \)( H.9.2). Kí hiệu đỉnh góc vuông là A, đỉnh góc 60\(^\circ \) là B và đỉnh góc 30\(^\circ \) là C.
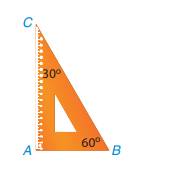
· Sắp xếp độ dài các cạnh theo thứ tự từ bé đến lớn. Sắp xếp độ lớn các góc theo thứ tự từ bé đến lớn.
· Góc lớn nhất đối diện với cạnh nào? Góc bé nhất đối diện với cạnh nào?
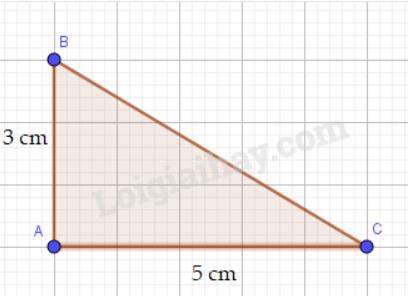
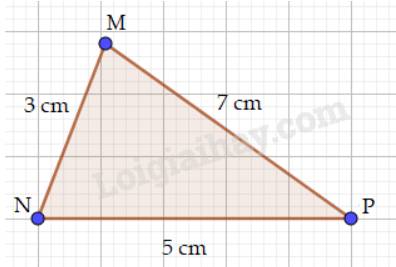
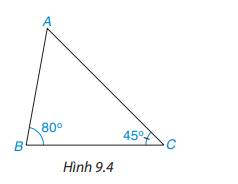


- AB < AC < BC nên sắp xếp độ dài các cạnh theo thứ tự từ bé đến lớn là: AB, AC, BC.
\(\widehat C < \widehat B < \widehat A\) nên sắp xếp độ lớn các góc theo thứ tự từ bé đến lớn là: \(\widehat C;\widehat B;\widehat A\)
- Góc lớn nhất là góc A đối diện với cạnh BC. Góc bé nhất là góc C đối diện với cạnh AB.
Trả lời bởi Hà Quang Minh