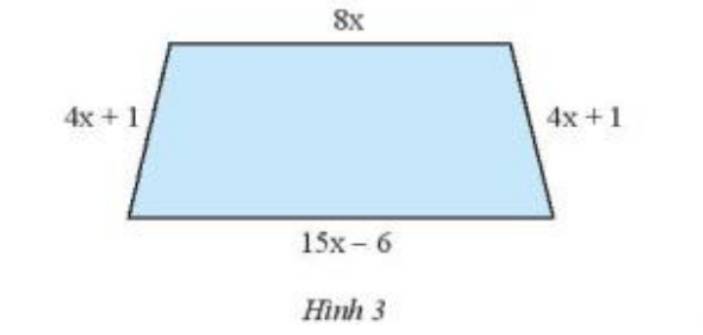
Viết biểu thức biểu thị chu vi của hình thang cân trong Hình 3.
Cho tam giác (xem Hình 4) có chu vi bằng 12t – 3. Tìm cạnh chưa biết của tam giác đó.
Ta có chu vi hình tam giác là :12t – 3
Cạnh cần tìm là : 12t – 3 – (3t + 8) – (4t – 7) = 5t – 4
Trả lời bởi Hà Quang MinhThực hiện phép tính \((x - 4) + \left[ {({x^2} + 2x) + (7 - x)} \right]\).
\(\begin{array}{l}(x - 4) + \left[ {({x^2} + 2x) + (7 - x)} \right]\\ = x - 4 + ({x^2} + 2x + 7 - x)\\ = x - 4 + {x^2} + 2x + 7 - x\\ = {x^2} + (x + 2x - x) + ( - 4 + 7)\\ = {x^2} + 2x + 3\end{array}\)
Trả lời bởi Hà Quang MinhCho đa thức A(y) = \( - 5{y^4} - 4{y^2} + 2y + 7\)
Tìm đa thức B(y) sao cho B(y) – A(y) = \(2{y^3} - 9{y^2} + 4y\)
\(B(y) - A(y) = 2{y^3} - 9{y^2} + 4y\)
\(\begin{array}{l}A(y) = - 5{y^4} - 4{y^2} + 2y + 7\\ \Rightarrow B(y) = 2{y^3} - 9{y^2} + 4y - 5{y^4} - 4{y^2} + 2y + 7\\ = - 5{y^4} + 2{y^3} - 13{y^2} + 6y + 7\end{array}\)
Trả lời bởi Hà Quang MinhCho hai đa thức P(x) = \( - 3{x^4} - 8{x^2} + 2x\) và Q(x) = \(5{x^3} - 3{x^2} + 4x - 6\).
Hãy tính P(x) + Q(x) và P(x) – Q(x).
\(P(x) + Q(x) = - 3{x^4} - 8{x^2} + 2x + 5{x^3} - 3{x^2} + 4x - 6\)
\( = - 3{x^4} + 5{x^3} + ( - 8{x^2} - 3{x^2}) + (2x + 4x) - 6\)
\( = - 3{x^4} + 5{x^3} - 11{x^2} + 6x - 6\)
\(P(x) - Q(x) = - 3{x^4} - 8{x^2} + 2x - 5{x^3} + 3{x^2} - 4x + 6\)
\( = - 3{x^4} - 5{x^3} + ( - 8{x^2} + 3{x^2}) + (2x - 4x) + 6\)
\( = - 3{x^4} - 5{x^3} - 5{x^2} - 2x + 6\)
Trả lời bởi Hà Quang MinhCho hai đa thức P(x) = \(2{x^3} - 9{x^2} + 5\) và Q(x) = \(2{x^2} + 4{x^3} - 7x\). Hãy tính P(x) – Q(x) bằng hai cách.
Tham khảo:
Cách 1 :
Ta có P(x) - Q(x)
= 2x3 – 9x2 + 5 – (2x2 + 4x3 – 7x)
= 2x3 – 9x2 + 5 – 2x2 – 4x3 + 7x
= (2x3 – 4x3) + (-9x2 – 2x2) + 7x + 5
= -2x3 – 11x2 + 7x + 5
Cách 2 :
P(x) = 2x3 – 9x2 + 5
Q(x) = 4x3 + 2x2 – 7x
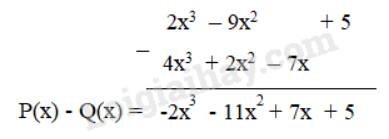
Cho hai đa thức P(x) = \(7{x^3} - 8x + 12\) và Q(x) = \(6{x^2} - 2{x^3} + 3x - 5\). Hãy tính P(x) + Q(x) bằng hai cách.
Tham khảo:
Cách 1:
P(x) + Q(x) = \(7{x^3} - 8x + 12 + 6{x^2} - 2{x^3} + 3x - 5\)
\(\begin{array}{l} = (7{x^3} - 2{x^3}) + 6{x^2} + ( - 8x + 3x) + (12 - 5)\\ = 5{x^3} + 6{x^2} - 5x + 7\end{array}\)
Cách 2:
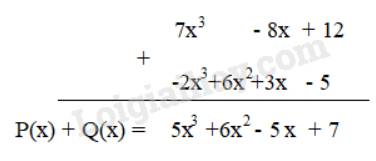
Hãy lập biểu thức biểu thị tổng chu vi hình vuông (Hình 1a) và hình chữ nhật (Hình 1b).
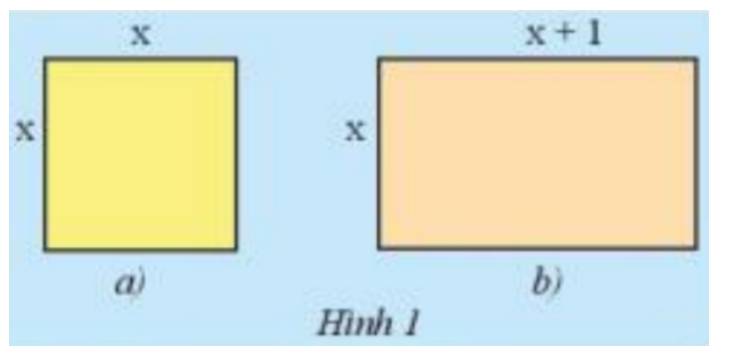
Chu vi hình vuông là \(4x\)
Chu vi hình chữ nhật là \(2.[x+(x + 1)]\)
\( \Rightarrow \) Tổng chu vi 2 hình là : \({4x}+2.[x.(x + 1)] = 4x + 2(2x+1) = 4x +4x + 2 = 8x+2\)
Trả lời bởi Hà Quang MinhHình 2 gồm một hình chữ nhật có chiều dài 4x cm, chiều rộng 2x cm và hình vuông nhỏ bên trong có cạnh x cm. Hãy lập biểu thức biểu thị diện tích của phần được tô màu vàng trong Hình 2.
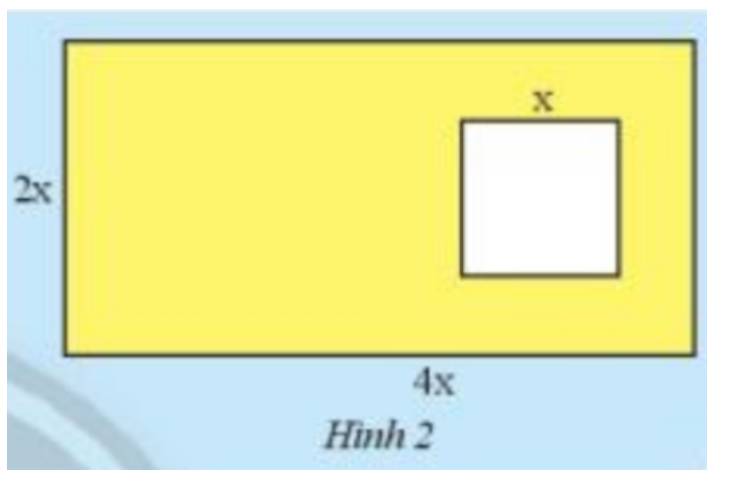
Diện tích hình chữ nhật là \(2x.4x = 8{x^2}\)
Diện tích phần hình vuông là \({x^2}\)
Diện tích phần màu vàng còn lại là \(8{x^2} - {x^2} = 7{x^2}\)
Trả lời bởi Hà Quang MinhCho đa thức M(x) = \(7{x^3} - 2{x^2} + 8x + 4\)
Tìm đa thức N(x) sao cho M(x) + N(x) = \(3{x^2} - 2x\)
Vì M(x) + N(x) = \(3{x^2} - 2x\)
Mà M(x) = \(7{x^3} - 2{x^2} + 8x + 4\)
Ta có: N(x) = M(x) + N(x) – M(x)
= \(3{x^2} - 2x - 7{x^3} + 2{x^2} - 8x - 4\)
\( = - 7{x^3} + 5{x^2} - 10x - 4\)
Trả lời bởi Hà Quang Minh
Ta có chu vi hình thang là :
C = \(8x + (15x - 6) + (4x + 1) + (4x + 1)\)
\( = 31x - 4\)
Trả lời bởi Hà Quang Minh