Tìm tổng của hai đa thức: x3 – 5x + 2 và x3 – x2 +6x – 4.
Bài 26. Phép cộng và phép trừ đa thức một biến
QL
Hướng dẫn giải
Thảo luận (2)
QL
Cho hai đa thức M = 0,5x4 – 4x3 + 2x – 2,5 và N = 2x3 + x2 + 1,5
Hãy tính tổng M + N (trình bày theo 2 cách)
Hướng dẫn giải
Thảo luận (1)
Cách 1:
M + N = (0,5x4 – 4x3 + 2x – 2,5) + ( 2x3 + x2 + 1,5)
= 0,5x4 – 4x3 + 2x – 2,5 + 2x3 + x2 + 1,5
= 0,5x4 + (– 4x3 + 2x3 ) + x2 + 2x + (-2,5 + 1,5)
= 0,5x4 + (– 2x3 ) + x2 + 2x + (-1)
= 0,5x4 – 2x3 + x2 + 2x – 1
Cách 2:

QL
Đặt tính cộng để tìm tổng của ba đa thức sau:
A = 2x3 – 5x2 + x – 7
B = x2 – 2x + 6
C = -x3 + 4x2 - 1
Hướng dẫn giải
Thảo luận (1)
QL
Cho hai đa thức P = x4 + 3x3 – 5x2 + 7x và Q = -x3 + 4x2 – 2x +1
Tìm hiệu P – Q bằng cách bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn.
Hướng dẫn giải
Thảo luận (1)
Ta có: P – Q = x4 + 3x3 – 5x2 + 7x – (-x3 + 4x2 – 2x +1)
= x4 + 3x3 – 5x2 + 7x + x3 - 4x2 - 4x2 + 2x – 1
= x4 + (3x3+ x3 ) + (– 5x2 - 4x2 ) + (7x + 2x ) – 1
= x4 + 4x3 – 9x2 + 9x – 1
Trả lời bởi Hà Quang Minh
QL
Cho hai đa thức P = x4 + 3x3 – 5x2 + 7x và Q = -x3 + 4x2 – 2x +1
Tìm hiệu P – Q bằng cách đặt tính trừ: đặt đa thức Q dưới đa thức P sao cho các hạng tử cùng bậc thẳng cột với nhau rồi trừ theo từng cột.
Hướng dẫn giải
Thảo luận (1)
QL
Cho hai đa thức:
M = 0,5x4 – 4x3 + 2x – 2,5 và N = 2x3 + x2 + 1,5
Hãy tính hiệu M - N (trình bày theo 2 cách)
Hướng dẫn giải
Thảo luận (1)
Cách 1:
M - N = (0,5x4 – 4x3 + 2x – 2,5) - ( 2x3 + x2 + 1,5)
= 0,5x4 – 4x3 + 2x – 2,5 - 2x3 - x2 - 1,5
= 0,5x4 + (– 4x3 - 2x3 ) - x2 + 2x + (-2,5 - 1,5)
= 0,5x4 + (– 6x3 ) - x2 + 2x + (-4)
= 0,5x4 – 6x3 - x2 + 2x – 4
Cách 2:
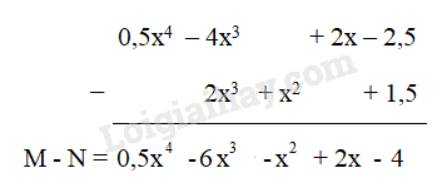
QL
Cho đa thức A = x4 – 3x2 – 2x + 1. Tìm các đa thức B và C sao cho:
A + B = 2x5 + 5x3 – 2
A – C = x3
Hướng dẫn giải
Thảo luận (1)
Ta có:
B = (A + B) – A = 2x5 + 5x3 – 2 – (x4 – 3x2 – 2x + 1)
= 2x5 + 5x3 – 2 – x4 + 3x2 + 2x - 1
= 2x5 – x4 + 5x3 + 3x2 + (-2 – 1)
= 2x5 – x4 + 5x3 + 3x2 – 3
C = A – (A – C) = x4 – 3x2 – 2x + 1 – x3
= x4 – x3– 3x2 – 2x + 1
Vậy B = 2x5 – x4 + 5x3 + 3x2 – 3
C = x4 – x3– 3x2 – 2x + 1
Trả lời bởi Hà Quang Minh
QL
Tìm tổng của hai đa thức sau bằng cách nhóm các hạng tử cùng bậc:
x2 – 3x + 2 và 4x3 – x2 + x - 1
Hướng dẫn giải
Thảo luận (1)
Ta có: (x2 – 3x + 2) + (4x3 – x2 + x – 1)
= x2 – 3x + 2 + 4x3 – x2 + x - 1
= 4x3 + (x2 – x2 ) + (-3x + x) + (2 – 1)
= 4x3 – 2x + 1
Trả lời bởi Hà Quang Minh
QL
Tìm hiệu sau theo cách đặt tính trừ: (- x3 – 5x + 2) – (3x + 8)
Hướng dẫn giải
Thảo luận (1)
QL
Cho hai đa thức:
\(A = 6{x^4} - 4{x^3} + x - \dfrac{1}{3};B = - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3}\)
Tính A + B và A - B
Hướng dẫn giải
Thảo luận (1)
\(\begin{array}{l}A + B = (6{x^4} - 4{x^3} + x - \dfrac{1}{3}) + ( - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3})\\ = 6{x^4} - 4{x^3} + x - \dfrac{1}{3} - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3}\\ = (6{x^4} - 3{x^4}) + ( - 4{x^3} - 2{x^3}) - 5{x^2} + (x + x) + ( - \dfrac{1}{3} + \dfrac{2}{3})\\ = 3{x^4} - 6{x^3} - 5{x^2} + 2x + \dfrac{1}{3}\\A - B = (6{x^4} - 4{x^3} + x - \dfrac{1}{3}) - ( - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3})\\ = 6{x^4} - 4{x^3} + x - \dfrac{1}{3} + 3{x^4} + 2{x^3} + 5{x^2} - x - \dfrac{2}{3}\\ = (6{x^4} + 3{x^4}) + ( - 4{x^3} + 2{x^3}) + 5{x^2} + (x - x) + ( - \dfrac{1}{3} - \dfrac{2}{3})\\ = 9{x^4} - 2{x^3} + 5{x^2} - 1\end{array}\)\(\begin{array}{l}A + B = (6{x^4} - 4{x^3} + x - \dfrac{1}{3}) + ( - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3})\\ = 6{x^4} - 4{x^3} + x - \dfrac{1}{3} - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3}\\ = (6{x^4} - 3{x^4}) + ( - 4{x^3} - 2{x^3}) - 5{x^2} + (x + x) + ( - \dfrac{1}{3} + \dfrac{2}{3})\\ = 3{x^4} - 6{x^3} - 5{x^2} + 2x + \dfrac{1}{3}\\A - B = (6{x^4} - 4{x^3} + x - \dfrac{1}{3}) - ( - 3{x^4} - 2{x^3} - 5{x^2} + x + \dfrac{2}{3})\\ = 6{x^4} - 4{x^3} + x - \dfrac{1}{3} + 3{x^4} + 2{x^3} + 5{x^2} - x - \dfrac{2}{3}\\ = (6{x^4} + 3{x^4}) + ( - 4{x^3} + 2{x^3}) + 5{x^2} + (x - x) + ( - \dfrac{1}{3} - \dfrac{2}{3})\\ = 9{x^4} - 2{x^3} + 5{x^2} - 1\end{array}\)
Trả lời bởi Hà Quang Minh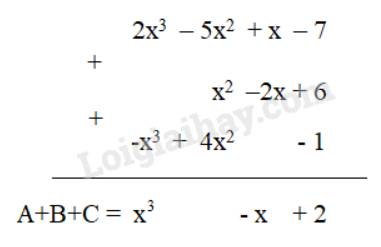
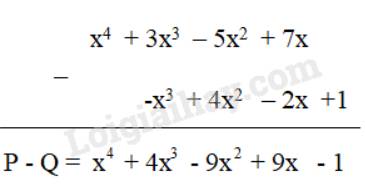
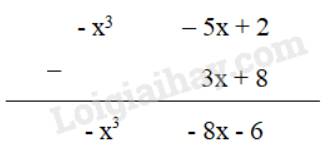
Cách 1:
(x3 – 5x + 2) + (x3 – x2 +6x – 4)
= x3 – 5x + 2 + x3 – x2 +6x – 4
=(x3 + x3 ) – x2 + (– 5x + 6x) + (2 – 4)
= 2x3 – x2 + x – 2
Cách 2:
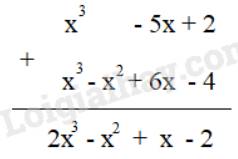
Trả lời bởi Kiều Sơn Tùng