Trên giá sách có 8 cuốn truyện ngắn, 7 cuốn tiểu thuyết và 5 tập thơ (tất cả đều khác nhau). Vẽ sơ đồ hình cây cho biết bạn Phong có bao nhiêu cách chọn một cuốn để đọc vào ngày cuối tuần.
Bài 23: Quy tắc đếm
QL
Hướng dẫn giải
Thảo luận (1)
QL
Một người gieo đồng xu hai mặt, sau mỗi lần gieo thì ghi lại kết quả là sấp hay ngửa. Hỏi nếu người đó gieo 3 lần thì có thể có bao nhiêu khả năng xảy ra?
Hướng dẫn giải
Thảo luận (1)
Mỗi lần gieo có 2 khả năng xảy ra: xấp hoặc ngửa
Nếu người đó gieo 3 lần thì có thể có số khả năng xảy ra là:
2.2.2 = 8 (khả năng)
Trả lời bởi Hà Quang Minh
QL
Để lắp ghế vào một phòng chiếu phim, các ghế được gắn nhãn bằng một chữ cái in hoa (trong bảng 26 chữ cái tiếng Anh Từ A đến Z) đứng trước và một số nguyên từ 1 đến 20, chẳng hạn X15, Z2,...
Hỏi có thể gắn nhãn tối đa được cho bao nhiêu ghế?
Hướng dẫn giải
Thảo luận (1)
Để gắn nhãn cho các ghế ta chọn chọn 1 chữ cái in hoa và 1 số (từ 1 đến 20).
Số cách chọn chữ cái in hoa: 26 cách (tương ứng với 26 chữ)
Số cách chọn số: 20 cách
Vậy số ghế gắn nhãn tối đa là 26.20 = 520 (ghế)
Trả lời bởi Hà Quang Minh
QL
Khối lớp 10 của một trường trung học phổ thông có ba lớp 10A, 10B, 10C. Lớp 10A có 30 bạn, lớp 10B có 35 bạn, lớp 10C có 32 bạn. Nhà trường muốn chọn 4 bạn để thành lập đội cờ đỏ của khối sao cho có đủ đại diện của các lớp. Hỏi có bao nhiêu cách lựa chọn?
Hướng dẫn giải
Thảo luận (1)
TH1: 2 bạn lớp 10A, 1 bạn lớp 10B, 1 bạn lớp 10C có số cách chọn là:
\(C_{30}^2\). 35. 32 = 487200( cách)
TH2: 1 bạn lớp 10A, 2 bạn lớp 10B, 1 bạn lớp 10C có số cách chọn là:
30.\(C_{35}^2\). 32 = 571200 (cách)
TH3: 1 bạn lớp 10A, 1 bạn lớp 10B, 2 bạn lớp 10C có số cách chọn là:
30. 35.\(C_{32}^2\) = 520800 (cách)
Vậy số cách lựa chọn là: 487200+ 571200 + 520800= 1579200 cách.
Trả lời bởi Hà Quang Minh
QL
Tại kì World Cup năm 2018, vòng bảng gồm có 32 đội tham gia, được chia vào 8 bảng, mỗi bảng 4 đội thi đấu vòng tròn (mỗi đội chơi một trận với từng đội khác trong cùng bảng). Hỏi tổng cộng vòng bảng có bao nhiêu trận đấu?
Hướng dẫn giải
Thảo luận (1)
- Mỗi bảng 4 đội thi đấu vòng tròn, giả sử là các đội A, B, C, D
Các trận đấu là: A-B, A-C, A-D, B-C, B-D, C-D => Có tất cả 6 trận đấu
- Có 8 bảng khác nhau.
- Tổng cộng vòng bảng có số trận đấu là 6.8 = 48 (trận đấu).
Trả lời bởi Hà Quang Minh
QL
Thầy Trung muốn đi từ Hà Nội vào Huế, rồi từ Huế vào Quảng Nam. Biết rằng từ Hà Nội vào Huế có thể đi bằng 3 cách: ô tô, tàu hỏa hoặc máy bay. Còn từ Huế vào Quảng Nam có thể đi bằng 2 cách: ô tô hoặc tàu hỏa.Hỏi thầy Trung có bao nhiêu cách chọn phương tiện để đi từ Hà Nội vào Quảng Nam?
Đọc tiếp
Thầy Trung muốn đi từ Hà Nội vào Huế, rồi từ Huế vào Quảng Nam. Biết rằng từ Hà Nội vào Huế có thể đi bằng 3 cách: ô tô, tàu hỏa hoặc máy bay. Còn từ Huế vào Quảng Nam có thể đi bằng 2 cách: ô tô hoặc tàu hỏa.
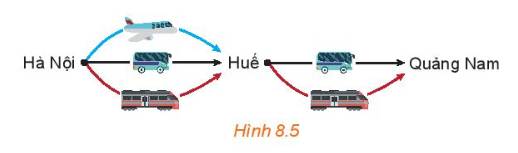
Hỏi thầy Trung có bao nhiêu cách chọn phương tiện để đi từ Hà Nội vào Quảng Nam?
Hướng dẫn giải
Thảo luận (1)
Đi từ Hà Nội vào Huế, rồi từ Huế vào Quảng Nam có các cách là:
Máy bay >> Oto
Máy bay >> tàu hỏa
Oto >> Oto
Oto >> tàu hỏa
Tàu hỏa >> Oto
Tàu hỏa >> tàu hỏa
Vậy thầy Trung có 6 cách chọn phương tiện để đi từ Hà Nội vào Quảng Nam.
Trả lời bởi Hà Quang Minh
QL
Chọn vé tàu (H.8.2) Bạn An đã quyết định mua vé tàu đi từ Hà Nội vào Vinh trên chuyến tàu SE7. Trên tàu có các toa ghế ngồi và các toa giường nằm. Toa ngồi có 2 loại vé: ngồi cứng và ngồi mềm. Toa nằm có loại không 4 giường và loại khoang 6 giường. Khoang 4 giường có hai loại vé: tầng 1 và tầng 2, khoang 6 giường có ba loại vé: tầng 1, tầng 2, tầng 3. Hỏi:a) Có bao nhiêu loại vé ghế ngồi và bao nhiêu loại vé giường nằm?b) Có bao nhiêu loại vé để bạn An lựa chọn?
Đọc tiếp
Chọn vé tàu (H.8.2)
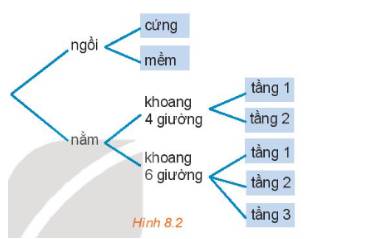
Bạn An đã quyết định mua vé tàu đi từ Hà Nội vào Vinh trên chuyến tàu SE7. Trên tàu có các toa ghế ngồi và các toa giường nằm. Toa ngồi có 2 loại vé: ngồi cứng và ngồi mềm. Toa nằm có loại không 4 giường và loại khoang 6 giường. Khoang 4 giường có hai loại vé: tầng 1 và tầng 2, khoang 6 giường có ba loại vé: tầng 1, tầng 2, tầng 3. Hỏi:
a) Có bao nhiêu loại vé ghế ngồi và bao nhiêu loại vé giường nằm?
b) Có bao nhiêu loại vé để bạn An lựa chọn?
Hướng dẫn giải
Thảo luận (1)
a) Số vé ghế ngồi là 2 (loại vé)
Số vé giường nằm là 2 + 3 = 5 (loại vé)
b) Số loại vé để bạn An lựa chọn là:
2 + 5 = 7 (loại vé)
Trả lời bởi Hà Quang Minh
QL
Chọn chuyến đi (H.8.1)
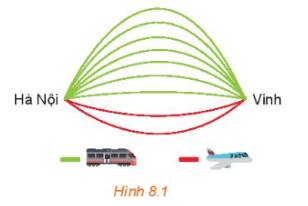
Từ Hà Nội vào Vinh mỗi ngày có 7 chuyến tàu hỏa và 2 chuyến máy bay. Bạn An muốn ngày Chủ nhật này đi từ Hà Nội vào Vinh bằng tàu hỏa hoặc máy bay.
Hỏi bạn An có bao nhiêu cách chọn?
Hướng dẫn giải
Thảo luận (1)
Để đi bằng tàu hỏa bạn An có 7 cách chọn và đi bằng máy bay có 2 cách chọn.
Vậy bạn An có tất cả 7 + 2 = 9 cách chọn chuyến đi.
Trả lời bởi Hà Quang Minh
QL
Có bao nhiêu số tự nhiên từ 1 đến 30 mà không nguyên tố cùng nhau với 35?
Hướng dẫn giải
Thảo luận (1)
Từ 1 đến 30 có:
- Có 6 số chia hết cho 5 là: 5, 10, 15, 20, 25, 30.
- Có 4 số chia hết cho 7 là: 7, 14, 21, 28.
Có tất cả 6+4= 10 số tự nhiên không nguyên tố cùng nhau với 35.
Trả lời bởi Hà Quang Minh
QL
Từ các chữ số 0, 1, 2, 3 có thể lập được bao nhiêu số thỏa mãn:
a) Là số tự nhiên có ba chữ số khác nhau?
b) Là số tự nhiên chẵn có ba chữ số khác nhau?
Hướng dẫn giải
Thảo luận (1)
a) Từ 4 chữ số 0, 1, 2, 3:
- Hàng trăm có 3 cách chọn.
- Hàng chục có 3 cách chọn.
- Hàng đơn vị có 2 cách chọn.
Vậy có tất cả 3.3.2 = 18 số tự nhiên khác nhau có 3 chữ số được lập từ 0, 1, 2, 3.
b) - Trường hợp 1: hàng đơn vị là số 0 như vậy hàng trăm có 3 cách chọn, hàng chục có 2 cách chọn.
Có tất cả 1. 2. 3 = 6 số có thể lập được.
- Trường hợp 2: hàng đơn vị là số 2 như vậy hàng trăm có 2 cách chọn, hàng chục có 2 cách chọn.
Có tất cả 1. 2. 2 = 4 số có thể lập được.
Vậy có thể lập 6 + 4 = 10 số tự nhiên chẵn có ba chữ số khác nhau.
Trả lời bởi Hà Quang Minh
Bạn Phong có số cách chọn một cuốn để đọc vào ngày cuối tuần là:
8 + 7 + 5 = 20 (cách)
Trả lời bởi Hà Quang Minh