Vẽ các elip sau
a) \(\frac{{{x^2}}}{{10}} + \frac{{{y^2}}}{4} = 1\)
b) \(\frac{{{x^2}}}{{12}} + \frac{{{y^2}}}{3} = 1\)
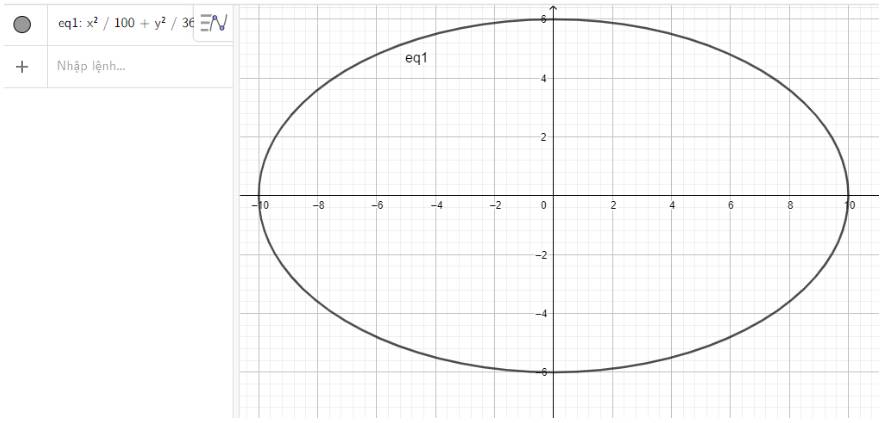
c) \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\)
Vẽ các elip sau
a) \(\frac{{{x^2}}}{{10}} + \frac{{{y^2}}}{4} = 1\)
b) \(\frac{{{x^2}}}{{12}} + \frac{{{y^2}}}{3} = 1\)
c) \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\)
Thiết kế một đường hầm có mặt cắt hình nửa elip cao 4 m, rộng 10 m.
Ta có: Chiều cao và chiều rộng của đường hầm là 4m, 10m nên ta có: \(a = 5,b = 4\)
Nên phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)
Nhập phương trình elip theo cú pháp x^2/25 + y^2/16 = 1 {y>=0} vào vùng nhập lệnh ta có hình vẽ mô phỏng đường hầm dưới đây
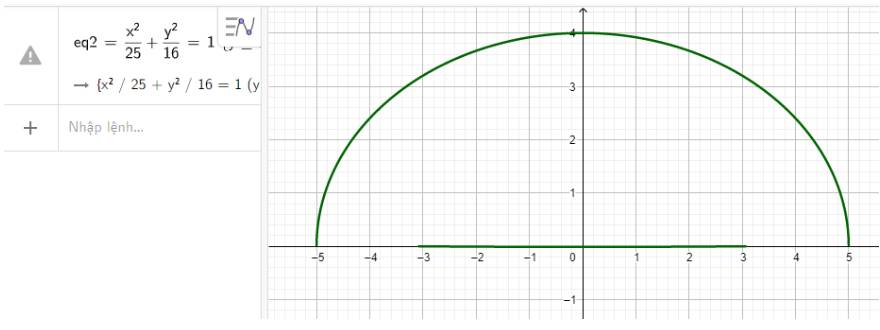
Vậy phương trình mô phỏng đường hầm là \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\) với \(y \ge 0\)
Và có hình mô phỏng thực tế như hình trên
Trả lời bởi Hà Quang MinhVẽ các hypebol sau:
a) \(\frac{{{x^2}}}{{10}} - \frac{{{y^2}}}{6} = 1\)
b) \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{3} = 1\)
c) \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\)
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình hypebol theo cú pháp x^2/10 - y^2/6 = 1 vào vùng nhập lệnh ta được hình hypebpl dưới đây:

b) Nhập phương trình hypebol theo cú pháp x^2/4 - y^2/3 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:
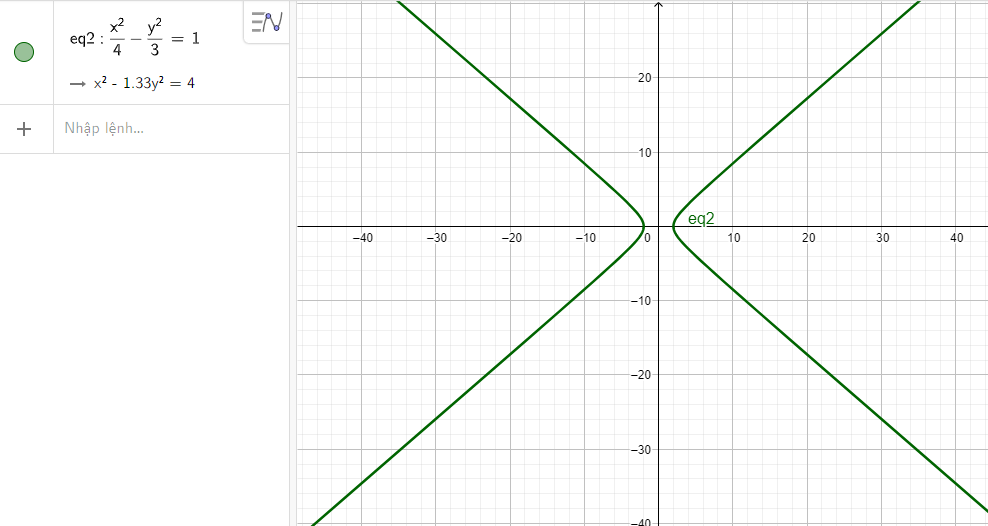
c) Nhập phương trình hypebol theo cú pháp x^2/64 - y^2/36 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:

Vẽ các parabol sau:
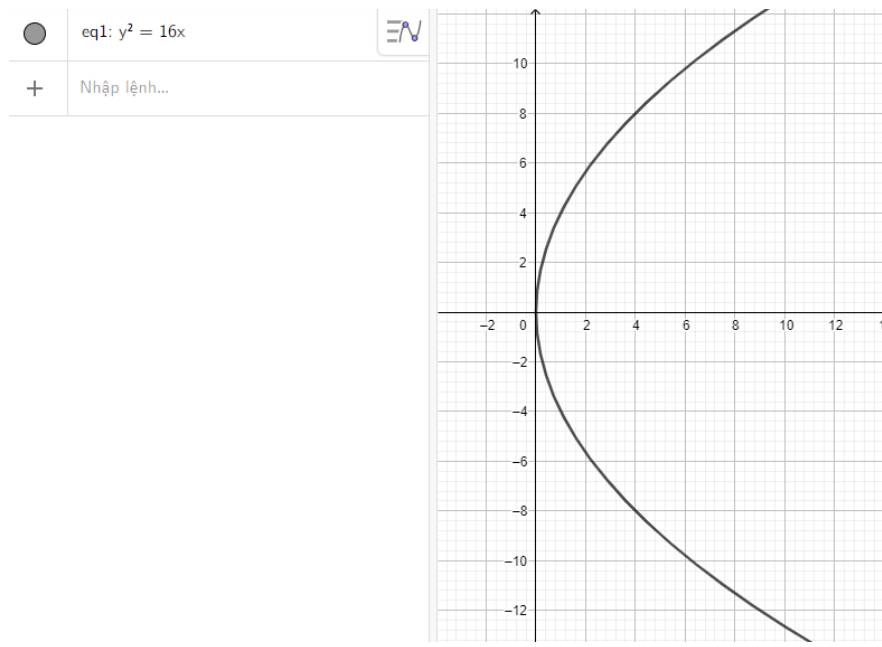
a) \({y^2} = 16x\)
b) \({y^2} = x\)
c) \({y^2} = 32x\)
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình parabol theo cú pháp y^2 = 16x vào vùng nhập lệnh ta được hình parabol dưới đây:
b) Nhập phương trình parabol theo cú pháp y^2 = x vào vùng nhập lệnh ta được hình parabol dưới đây:

c) Nhập phương trình parabol theo cú pháp y^2 = 32x vào vùng nhập lệnh ta được hình parabol dưới đây:

Thiết kế một chóa đèn có mặt cắt hình parabol với kích thước được cho trong hình sau:

Chóa đèn có hình dạng parabol nên phương trình mô phỏng chóa đèn có dạng \({y^2} = 2px\)
Gắn hệ tọa độ Oxy vào chóa đèn với gốc tọa độ tại đỉnh chóa đèn, suy ta phương trình đó đi qua điểm có tọa độ (3; 9)
Thay tọa độ điểm (3; 9) vào phương trình \({y^2} = 2px\), ta có \({9^2} = 2p.3 \Rightarrow p = \frac{{27}}{2}\)
Suy ra phương trình mô tả chóa đèn là \({y^2} = 27x\) với \(x \le 3\)
Hình ảnh mô phỏng chóa đèn có dạng như hình dưới:
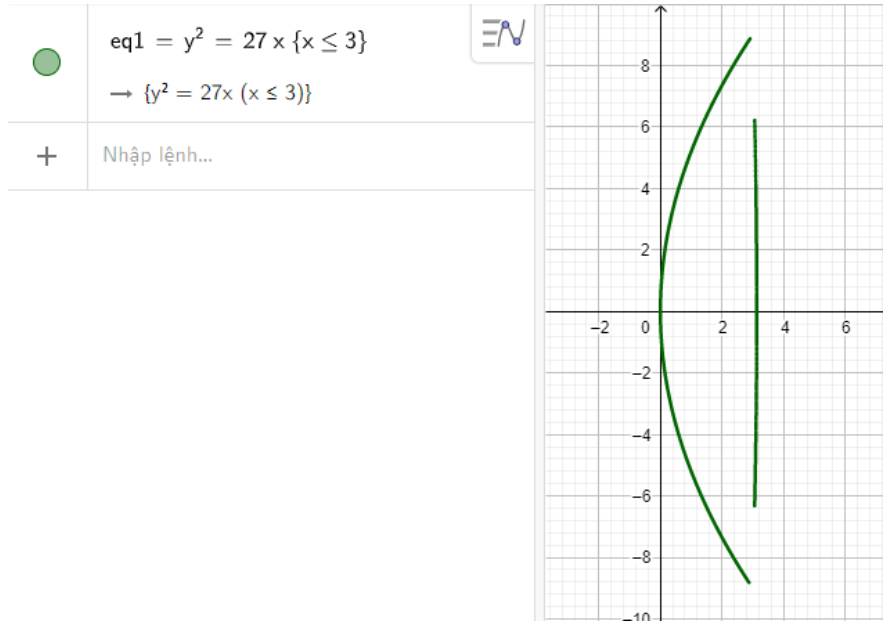
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình elip theo cú pháp x^2/10 + y^2/4 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
b) Nhập phương trình elip theo cú pháp x^2/12 + y^2/3 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
c) Nhập phương trình elip theo cú pháp x^2/100 + y^2/36 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
Trả lời bởi Hà Quang Minh