Trong giờ học môn Mĩ thuật, bạn Hạnh dán lên trang vở hai hình vuông có kích thước lần lượt là 3 cm và x cm như ở Hình 1. Tổng diện tích của hai hình vuông đó là \({x^2} + 9(c{m^2})\).
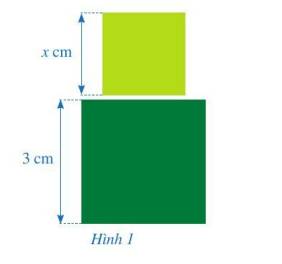
Biểu thức đại số \({x^2} + 9\)có gì đặc biệt?
Trong giờ học môn Mĩ thuật, bạn Hạnh dán lên trang vở hai hình vuông có kích thước lần lượt là 3 cm và x cm như ở Hình 1. Tổng diện tích của hai hình vuông đó là \({x^2} + 9(c{m^2})\).

Biểu thức đại số \({x^2} + 9\)có gì đặc biệt?
a) Viết biểu thức biểu thị:
- Diện tích hình vuông có độ dài cạnh là x cm;
- Thể tích của hình lập phương có độ dài cạnh là 2x cm.
b) Các biểu thức trên có dạng như thế nào?
a) Biểu thức biểu thị:
- Diện tích hình vuông có độ dài cạnh là x cm là \(x.x = {x^2}(c{m^2})\)
- Thể tích của hình lập phương có độ dài cạnh là 2x cm là \({(2x)^3} = 8{x^3}(c{m^3})\)
b) Các biểu thức trên có dạng một biến với lũy thừa có số mũ nguyên dương của biến đó.
Trả lời bởi Hà Quang Minha) Viết biểu thức biểu thị:
- Quãng đường ô tô đi được trong thời gian x (h), nếu vận tốc là 60 km/h;
- Tổng diện tích của các hình: hình vuông có độ dài cạnh là 2x cm; hình chữ nhật có các kích thước là 3 cm và x cm; hình thoi có độ dài hai đường chéo là 4 cm và 8 cm.
b) Các biểu thức trên có bao nhiêu biến? Mỗi số hạng xuất hiện trong biểu thức có dạng như thế nào?
a) Biểu thức biểu thị:
- Quãng đường ô tô đi được trong thời gian x (h), nếu vận tốc là 60 km/h là \(60x\) (km).
- Tổng diện tích của các hình: hình vuông có độ dài cạnh là 2x cm; hình chữ nhật có các kích thước là 3 cm và x cm; hình thoi có độ dài hai đường chéo là 4 cm và 8 cm là
\({(2x)^2} + 3.x + \dfrac{1}{2}.4.8 = 4{x^2} + 3x + 16\)
b) Các biểu thức trên có 1 biến (biến x). Mỗi số hạng xuất hiện trong biểu thức (60x, 4x2, 3x) đều là tích của một số nhân một biến và số hạng (8) là dạng số hoặc đơn thức với số mũ của x bằng 0.
Trả lời bởi Hà Quang MinhBiểu thức nào sau đây là đa thức một biến?
a) \({x^2} + 9;\)
b) \(\dfrac{2}{{{x^2}}} + 2x + 1;\)
c) \(3x + \dfrac{2}{5}y.\)
a) \({x^2} + 9\) là đa thức một biến x.
b) \(\dfrac{2}{{{x^2}}} + 2x + 1\) không phải là đa thức một biến x.
c) \(3x + \dfrac{2}{5}y\) không phải là đa thức một biến x hay y.
Trả lời bởi Hà Quang MinhCho hai đơn thức của cùng biến x là \(2{x^2}\)và \(3{x^2}\).
a) So sánh số mũ của biến x trong hai đơn thức trên.
b) Thực hiện phép cộng \(2{x^2} + 3{x^2}\).
c) So sánh kết quả của hai phép tính: \(2{x^2} + 3{x^2}\) và \((2 + 3){x^2}\).
a) Ta thấy: số mũ của x trong hai đơn thức trên bằng nhau (đều bằng 2).
b) \(2{x^2} + 3{x^2} = {x^2} + {x^2} + {x^2} + {x^2} + {x^2} = 5{x^2}\) .
c) Ta có: \((2 + 3){x^2} = 5{x^2}\).
Vậy \(2{x^2} + 3{x^2}\) = \((2 + 3){x^2}\).
Trả lời bởi Hà Quang MinhThực hiện mỗi phép tính sau:
a) \({x^2} + \dfrac{1}{4}{x^2} - 5{x^2}\);
b) \({y^4} + 6{y^4} - \dfrac{2}{5}{y^4}\).
a) \({x^2} + \dfrac{1}{4}{x^2} - 5{x^2} = (1 + \dfrac{1}{4} - 5){x^2} = - \dfrac{{15}}{4}{x^2}\);
b) \({y^4} + 6{y^4} - \dfrac{2}{5}{y^4} = (1 + 6 - \dfrac{2}{5}){y^4} = \dfrac{{33}}{5}{y^4}\).
Trả lời bởi Hà Quang MinhCho đa thức \(P(x) = {x^2} + 2{x^2} + 6x + 2x - 3\).
a) Nêu các đơn thức của biến x có trong đa thức P(x).
b) Tìm số mũ của biến x trong từng đơn thức nói trên.
c) Thực hiện phép cộng các đơn thức có cùng số mũ của biến x sao cho trong đơn thức P(x) không còn hai đơn thức nào có cùng số mũ của biến x.
a) Các đơn thức của biến x có trong đa thức P(x) là: \({x^2},2{x^2},6x,2x,( - 3)\).
b) Số mũ của biến x trong các đơn thức \({x^2},2{x^2},6x,2x,( - 3)\) lần lượt là: 2; 2; 1; 1; 0.
c) \(P(x) = {x^2} + 2{x^2} + 6x + 2x - 3 = ({x^2} + 2{x^2}) + (6x + 2x) - 3 = 3{x^3} + 8x - 3\).
Trả lời bởi Hà Quang MinhThu gọn đa thức
\(P(y) = - 2{y^3} + y + \dfrac{{11}}{7}{y^3} + 3{y^2} - 5 - 6{y^2} + 9\).
\(\begin{array}{l}P(y) = - 2{y^3} + y + \dfrac{{11}}{7}{y^3} + 3{y^2} - 5 - 6{y^2} + 9 = ( - 2{y^3} + \dfrac{{11}}{7}{y^3}) + (3{y^2} - 6{y^2}) + y + ( - 5 + 9)\\ = - \dfrac{3}{7}{y^3} - 3{y^2} + y + 4\end{array}\)
Trả lời bởi Hà Quang MinhCho đa thức \(R(x) = - 2{x^2} + 3{x^2} + 6x + 8{x^4} - 1\).
a) Thu gọn đa thức R(x).
b) Trong dạng thu gọn của đa thức R(x), sắp xếp các đơn thức theo số mũ giảm dần của biến.
a) \(R(x) = - 2{x^2} + 3{x^2} + 6x + 8{x^4} - 1 = ( - 2{x^2} + 3{x^2}) + 6x + 8{x^4} - 1 = {x^2} + 6x + 8{x^4} - 1\).
b) Trong các đơn thức của đa thức R(x) ta thấy, số mũ lớn nhất là 4, sau đó đến 2; 1 và 0.
Vậy \(R(x) = {x^2} + 6x + 8{x^4} - 1 = 8{x^4} + {x^2} + 6x - 1\).
Trả lời bởi Hà Quang MinhSắp xếp đa thức
\(H(x) = - 0,5{x^8} + 4{x^3} + 5{x^{10}} - 1\) theo:
a) Số mũ giảm dần của biến;
b) Số mũ tăng dần của biến.
a) \(H(x) = - 0,5{x^8} + 4{x^3} + 5{x^{10}} - 1 = 5{x^{10}} - 0,5{x^8} + 4{x^3} - 1\).
b) \(H(x) = - 0,5{x^8} + 4{x^3} + 5{x^{10}} - 1 = - 1 + 4{x^3} - 0,5{x^8} + 5{x^{10}}\).
Trả lời bởi Hà Quang Minh
Biểu thức đại số \({x^2} + 9\) xuất hiện biến x trong phép tính tính tổng diện tích của hai hình vuông.
Trả lời bởi Hà Quang Minh