Cho góc nhọn \(\widehat{xBy}=\alpha\). Xét tam giác ABC vuông tại A, tam giác A’BC’ vuông tại A’ với A, A’ thuộc tia Bx và C, C’ thuộc tia By (Hình 1). Do ∆ABC ᔕ ∆A’BC’ nên \(\dfrac{AC}{BC}=\dfrac{A'C'}{B'C'}\). Như vậy, tỉ số giữa cạnh đối AC của góc nhọn α và cạnh huyền BC trong tam giác vuông ABC không phụ thuộc vào việc chọn tam giác vuông đó.
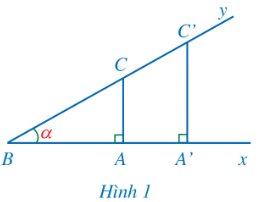
Tỉ số \(\dfrac{AC}{BC}\) có mối liên hệ như thế nào với độ lớn góc α?
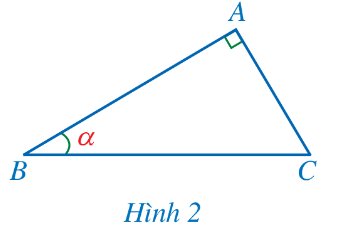
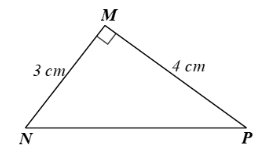
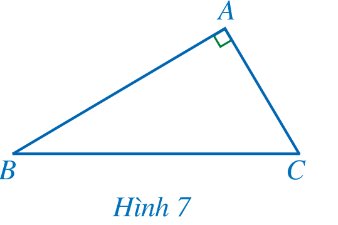


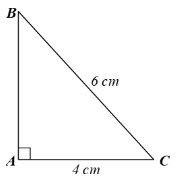
Xét ∆ABC vuông tại A, theo định nghĩa tỉ số lượng giác sin, ta có: \(\dfrac{AC}{BC}\) = sin α.
Trả lời bởi datcoder