$4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

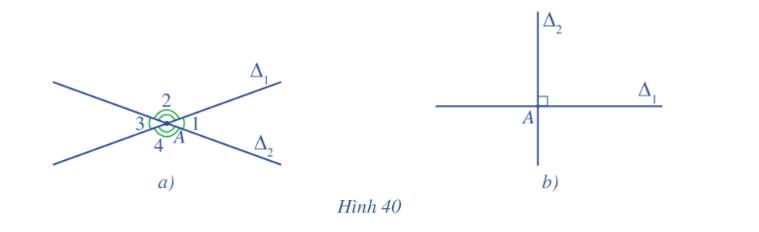
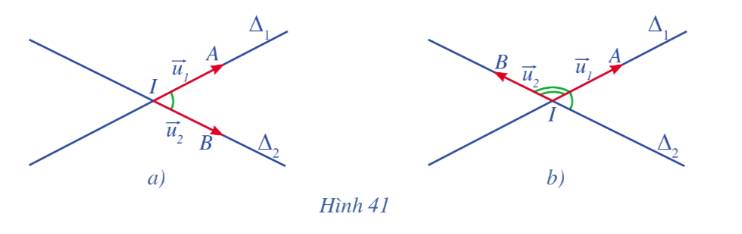
a) - Ta có: \(\overrightarrow {{u_1}}  = \left( {3\sqrt 3 ;3} \right);\overrightarrow {{u_2}}  = \left( {1 ;0} \right) \Rightarrow \cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right)} \right| = \frac{{\left| {3\sqrt 3 .1 + 3.0} \right|}}{{\sqrt {{{\left( {3\sqrt 3 } \right)}^2} + {3^2}} .\sqrt {{1^2} + {0^2}} }} = \frac{{\sqrt 3 }}{2}.\)

- Vậy \(\left( {{\Delta _1},{\Delta _2}} \right) = {30^o}\)

b) – Ta có\(\overrightarrow {{n_1}}  = \left( {2; - 1} \right);\overrightarrow {{n_2}}  = \left( { - 1  ;3} \right) \Rightarrow \cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {2.\left( { - 1} \right) + \left( { - 1} \right).3} \right|}}{{\sqrt {{{\left( 2 \right)}^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{{\left( 1 \right)}^2} + {3^2}} }} = \frac{{\sqrt 2 }}{2}.\)

- Vậy \(\left( {{\Delta _1},{\Delta _2}} \right) = {45^o}\)

a) Do MH vuông góc với đường thẳng \(\Delta \) nên ta có vecto chỉ phương của MH là: \(\overrightarrow u  = \left( {2;1} \right)\)

b) Phương trình tham số của đường thẳng MH đi qua \(M\left( { - 1;1} \right)\) có vecto chỉ phương\(\overrightarrow u  = \left( {2;1} \right)\) là: \(\left\{ \begin{array}{l}x =  - 1 + 2t\\y = 1 + t\end{array} \right. \Leftrightarrow x - 2y + 3 = 0\)

c) H là giao điểm của MH và đường thẳng \(\Delta \)

Xét hệ phương trình: \(\left\{ \begin{array}{l}x - 2y + 3 = 0\\2x + y - 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\) . Vậy tọa độ điểm H là: \(H\left( {1;2} \right)\)

Độ dài đoạn thẳng MH là: \(MH = \sqrt {{{\left( {1 + 1} \right)}^2} + {{\left( {2 - 1} \right)}^2}}  = \sqrt {{2^2} + {1^2}}  = \sqrt 5 \)

Xét hệ phương trình gồm phương trình của d và \({\Delta _1}\) ta có: \(\left\{ \begin{array}{l}x + 2y - 2 = 0\\3x - 2y + 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 1\\y = \frac{3}{2}\end{array} \right.\)

Vậy d và \({\Delta _1}\) cắt nhau tại 1 điểm duy nhất.

Xét hệ phương trình gồm phương trình của d và \({\Delta _2}\) ta có: \(\left\{ \begin{array}{l}x + 2y - 2 = 0\\x + 2y + 2 = 0\end{array} \right.\).  Hệ phương trình vô nghiệm.

Vậy d và \({\Delta _2}\) song song với nhau

Xét hệ phương trình gồm phương trình của d và \({\Delta _3}\) ta có: \(\left\{ \begin{array}{l}x + 2y - 2 = 0\\2x + 4y--4{\rm{ }} = {\rm{ }}0\end{array} \right.\). Hệ phương trình vô số nghiệm.

Vậy d và \({\Delta _3}\) trùng nhau.

Ta có: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {{u_1}} ;\overrightarrow {{u_2}} } \right)} \right| = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}.\)

Trong hình 40a, ta có góc \(\widehat {{A_1}}\) là một góc nhọn.

Trong hình 40b thì ta có 4 góc tại đỉnh A là một góc vuông.

Ta có: \(\overrightarrow {{u_1}}  = \left( {1;1} \right),\overrightarrow {{u_2}}  = \left( {2;2} \right)\). Ta thấy, \(\overrightarrow {{u_2}}  = 2\overrightarrow {{u_1}} \).

Chọn điểm \(A\left( {1; - 2} \right) \in {\Delta _1}\). Thay tọa độ điểm A vào phương trình đường thẳng \({\Delta _2}\) ta được \({t_2} = \frac{1}{2} \Rightarrow A\left( {1; - 2} \right) \in {\Delta _2}\).

Vậy 2 đường thẳng \({\Delta _1}\) và \({\Delta _2}\) song song với nhau.

Hai đường thẳng trong mặt phẳng thì cắt nhau hoặc song song hoặc trùng nhau.

Để xác định điểm M ta cần giải hệ phương trình gồm hai phương trình đường thẳng của hai đường thẳng a và b

Trong mặt phẳng toạ độ, cho hai đường thẳng \({\Delta _1},{\Delta _2}\)  lần lượt có vectơ chỉ phương là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \). Khi đó:

a) \({\Delta _1}\) cắt \({\Delta _2}\) khi và chỉ khi \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) không cùng phương.

b) \({\Delta _1}\) song song với \({\Delta _2}\) khi và chỉ khi \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) cùng phương và có một điểm thuộc một đường thẳng mà không thuộc đường thẳng còn lại.

c) \({\Delta _1}\) trùng với \({\Delta _2}\) khi và chỉ khi \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) cùng phương và có một điểm thuộc cả hai đường thẳng đó.

a) Độ lớn của góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) và độ lớn của góc giữa hai vectơ \(\overrightarrow {IA} \),\(\overrightarrow {IB} \)có thể bẳng nhau hoặc bù nhau.

b) Nếu \(\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) \le {90^o}\)thì \(\left( {{\Delta _1},{\Delta _2}} \right) = \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\). Do đó,\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\) và \(\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) \ge 0\).

Nếu \(\left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) > {90^o}\)thì \(\left( {{\Delta _1},{\Delta _2}} \right) = {180^o} - \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\). Do đó,\(\cos \left( {{\Delta _1},{\Delta _2}} \right) =  - \cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)\) và \(\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right) < 0\).

Vậy ta có: \(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \left| {\cos \left( {\overrightarrow {IA} ,{\rm{ }}\overrightarrow {IB} } \right)} \right|\)