SEA Games 30 đã đi vào lịch sử của Thể thao Việt Nam. Lần đầu tiên, Việt Nham cùng được huy chương Vàng cả bóng đá nam và bóng đá nữ. Đặc biệt, số bàn thắng trung bình của đội tuyển bóng đã nam U22 Việt Nam trong mỗi trận đấu là 3,43.
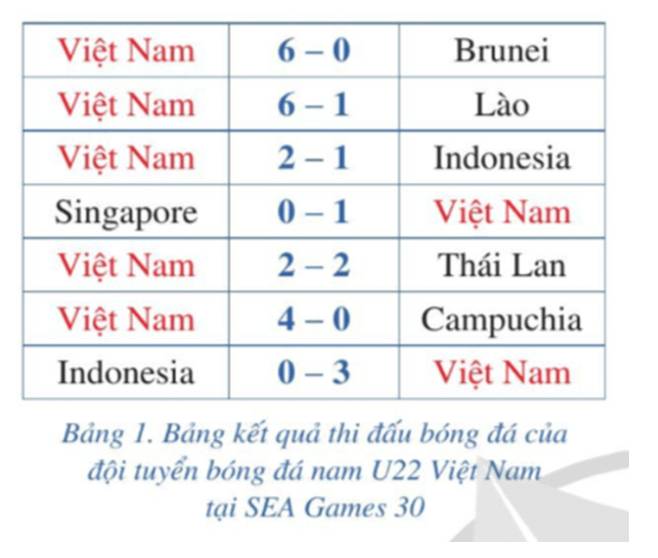
Số bàn thắng trung bình trong mỗi trận đấu được tính như thế nào?
Số bàn thắng trung bình trong mỗi trận đấu được tính bằng tổng cộng số bàn thắng của tất cả các trận đấu rồi chia cho số trận đấu.
Số bàn thắng trung bình trong mỗi trận đấu \( = \frac{{6 + 6 + 2 + 1 + 2 + 4 + 3}}{7} = 3,43\)
Trả lời bởi Hà Quang Minh