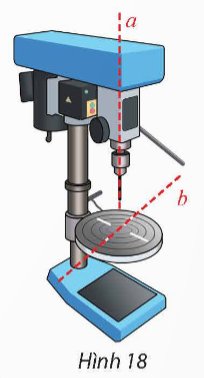
Trên phần mềm mô phỏng 3D một máy khoan trong không gian Oxyz, cho biết phương trình trục a của mũi khoan và một đường rãnh b trên vật cần khoan (Hình 18) lần lượt là:
\(a:\left\{{}\begin{matrix}x=1\\y=2\\z=3t\end{matrix}\right.\) và \(b:\left\{{}\begin{matrix}x=1+4t'\\y=2+2t'\\z=6\end{matrix}\right.\).
a) Chứng minh a, b vuông góc và cắt nhau.
b) Tìm giao điểm của a và b.
a, VTCP a : (0;0;3)
VTCP b : (4;2;0)
=> VTCP a . VTCP b = 0
=> a vuông góc b
Lại có [VTCPa.VTCPb] . vectơAB =0 ( với A là điểm thuộc a, B là điểm thuộc b )
=> a;b cắt nhau
b, Cho H là điểm giao giữa a;b => H(1;2;3t)
Ta có \(\left\{{}\begin{matrix}1+4t'=1\\2+2t'=2\\3t=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}t'=0\\t'=0\\t=2\end{matrix}\right.\)
Với t = 2 => H(1;2;6)


