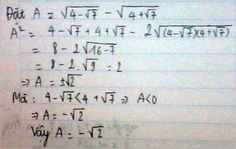Question

Tính

\(\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}\)

Answer 1

\(\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}\\ =\dfrac{1}{\sqrt{2}}\left(\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\right)\\ =\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(\sqrt{7}+1\right)^2}\right)\\ =\dfrac{1}{\sqrt{2}}\left(\left|\sqrt{7}-1\right|-\left|\sqrt{7}+1\right|\right)\\ =\dfrac{1}{\sqrt{2}}\left(\sqrt{7}-1-\sqrt{7}-1\right)\\ =\dfrac{1}{\sqrt{2}}\cdot\left(-2\right)=-\sqrt{2}\)

Answer 2

❤✔✔❤

Answer 3

Đặt biểu thức là A.

Ta có: \(A^2=4-\sqrt{7}-2\sqrt{\left(4+\sqrt{7}\right)\left(4-\sqrt{7}\right)}+4+\sqrt{7}=8-2\sqrt{16-7}=8-6=2\Rightarrow A=\pm2\)

Nhưng do A < 0 nên A = \(-\sqrt{2}\)