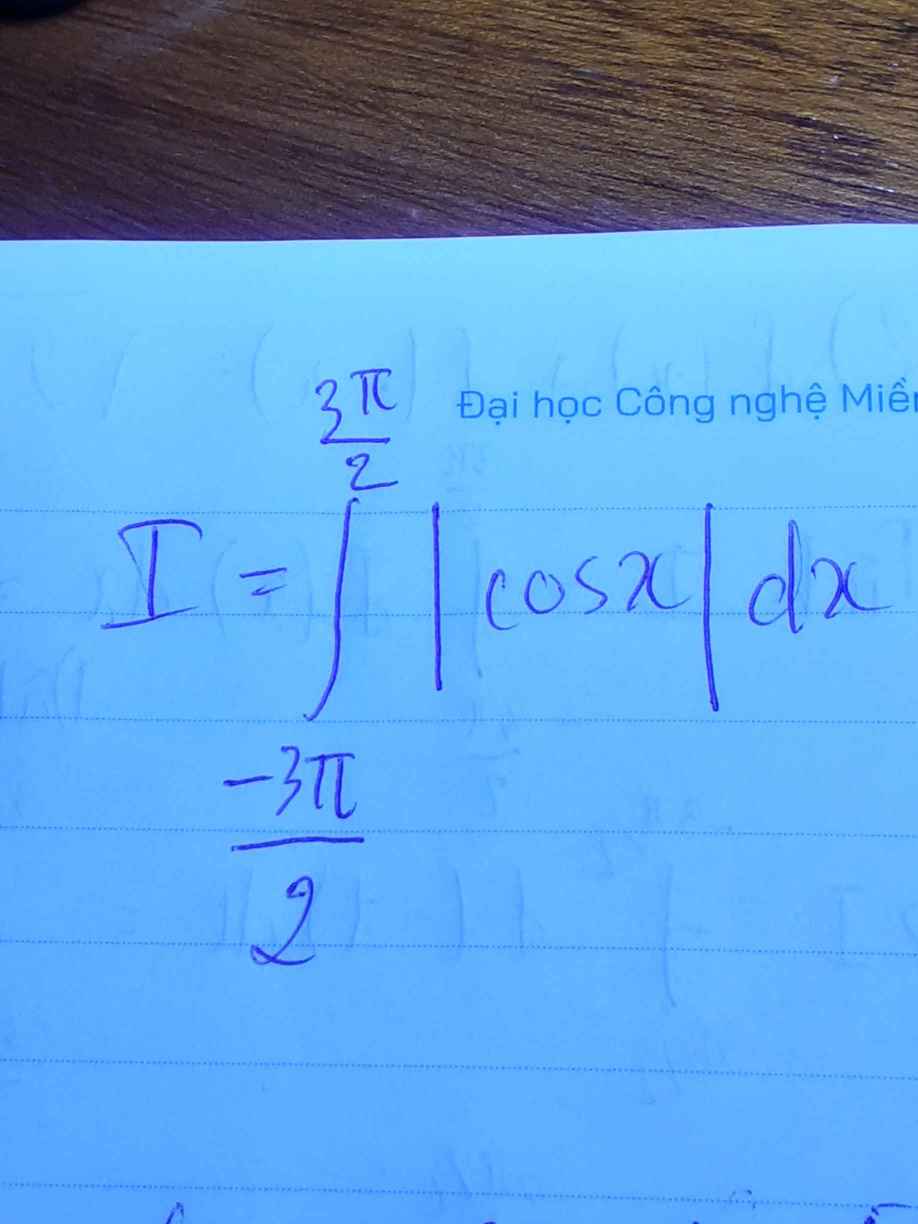Trên \(\left[-\dfrac{3\pi}{2};\dfrac{3\pi}{2}\right]\) ta có: \(cosx\ge0\) khi \(-\dfrac{\pi}{2}\le x\le\dfrac{\pi}{2}\)
\(cosx\le0\) khi \(-\dfrac{3\pi}{2}\le x\le-\dfrac{\pi}{2}\) và \(\dfrac{\pi}{2}\le x\le\dfrac{3\pi}{2}\)
Do đó:
\(\int\limits^{\dfrac{3\pi}{2}}_{-\dfrac{3\pi}{2}}\left|cosx\right|dx=\int\limits^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}\left(-cosx\right)dx+\int\limits^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}cosxdx+\int\limits^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}\left(-cosx\right)dx\)
\(=-sinx|^{-\dfrac{\pi}{2}}_{-\dfrac{3\pi}{2}}+sinx|^{\dfrac{\pi}{2}}_{-\dfrac{\pi}{2}}-sinx|^{\dfrac{3\pi}{2}}_{\dfrac{\pi}{2}}=2+2+2=6\)
Đúng 3
Bình luận (0)
