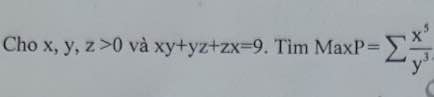Lời giải:
\(\left\{\begin{matrix} x^2+y^2=9\\ x^3+y^3=-27\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (x+y)^2-2xy=9\\ (x+y)^3-3xy(x+y)=-27\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} a^2-2b=9\\ a^3-3ab=-27\end{matrix}\right.\) (đặt $x+y=a; xy=b)$
\(\Leftrightarrow \left\{\begin{matrix} 2b=a^2-9\\ 2a^3-6ab+54=0\end{matrix}\right.\)
\(\Rightarrow 2a^3-3a(a^2-9)+54=0\)
\(\Leftrightarrow -a^3+27a+54=0\)
\(\Leftrightarrow (a+3)^2(a-6)=0\Rightarrow a=-3\) hoặc $a=6$
Nếu $a=-3\Rightarrow b=0$
$\Leftrightarrow x+y=-3; xy=0$. Theo định lý Viet đảo thì $x,y$ là nghiệm của pt $X^2+3X=0$
$\Leftrightarrow (x,y)=(0,-3); (-3,0)$
Nếu $a=x+y=6\Rightarrow b=xy=\frac{27}{2}$. Theo định lý Viet đảo thì $x,y$ là nghiệm của pt $X^2-6X+\frac{27}{2}=0$ (pt này vô nghiệm nên loại)
Vậy.........