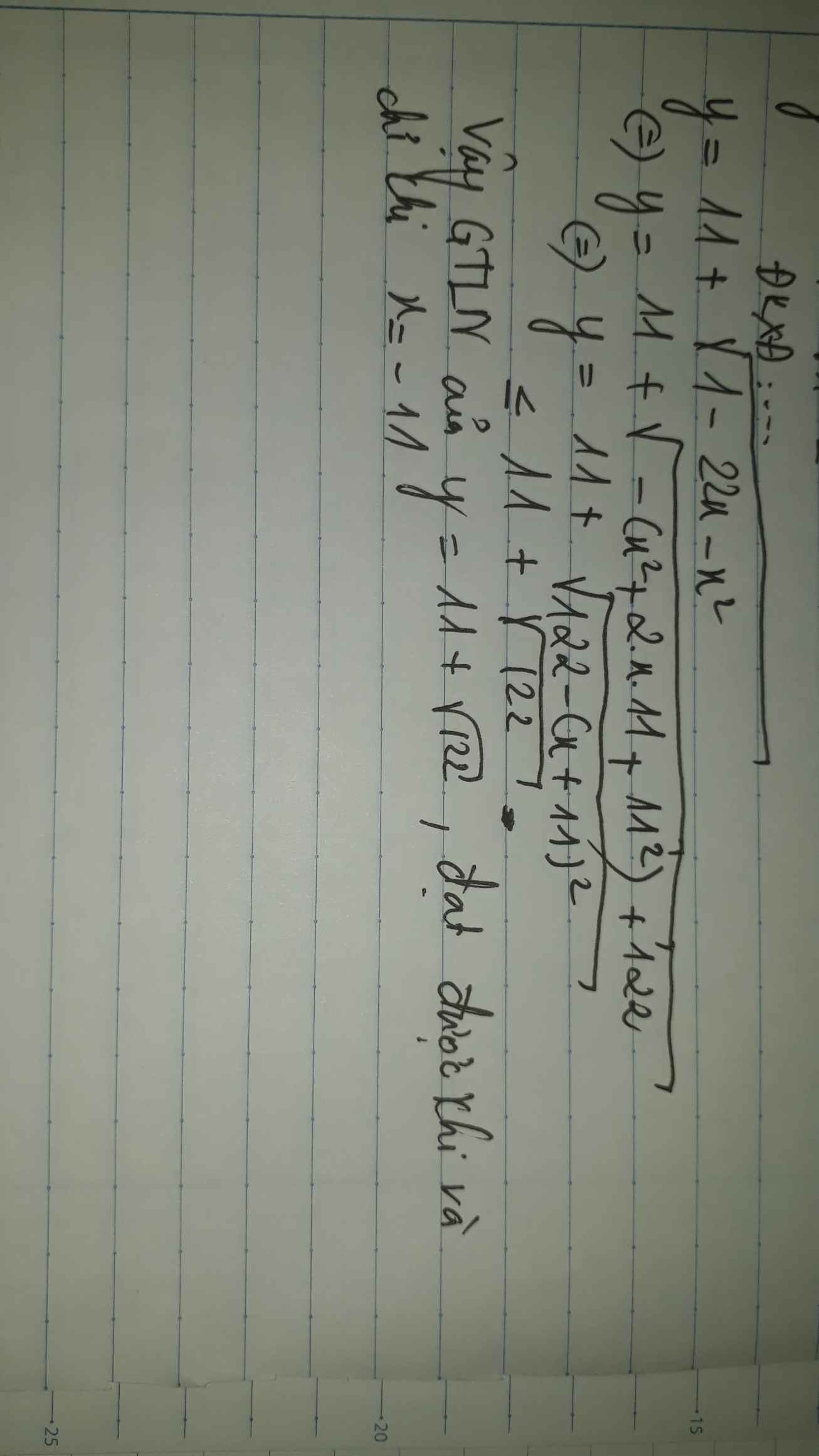Ôn thi vào 10
Các câu hỏi tương tự
Cho x, y không âm và x+y ≤1. Tìm GTLN của \(A=\sqrt{1+4x^2}+\sqrt{1+4y^2}+3\sqrt{x}+3\sqrt{y}\)
Mọi người giúp em với, xin cảm ơn ạ.
Cho x,y,z là các số dương thỏa mãn x+y+z=1. Tìm GTLN của P = \(\sqrt{x+yz}+\sqrt{y+xz}+\sqrt{z+xy}\)
Tìm GTLN của \(x\sqrt{1-x^2}\)
Tìm GTLN của P= \(\dfrac{\sqrt{x}+3}{\sqrt{x}+1}\)
Tìm GTLN và GTNN của A= 3\(\sqrt{x-1}+4\sqrt{5-x}\) với 1≤x≤5
Cho \(D=\dfrac{2\sqrt{x}+7}{\sqrt{x}-1}\)
Tìm số tự nhiên x để D đạt GTLN
VH
6 tháng 5 2021 lúc 22:56
Cho a,b,c dương thỏa mãn : \(a+b+c\le3\)
Tìm GTLN của biểu thức
\(B=\sqrt{1+a^2}+\sqrt{1+b^2}+\sqrt{1+c^2}+2\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)\)
Cho biểu thức P = \(\dfrac{4\sqrt{x}+3}{x+1}\) ( x lớn hơn hoặc bàng 0 )
Tìm GTNN và GTLN của P
cho x,y,z là số dương thỏa mãn x+y+z ≤3 tìm giá trị lớn nhất của biểu thức
P=\(\sqrt{1+x^2}+\sqrt{1+y^2}+\sqrt{1+z^2}+2\left(\sqrt{x}+\sqrt{y}+\sqrt{z}\right)\)