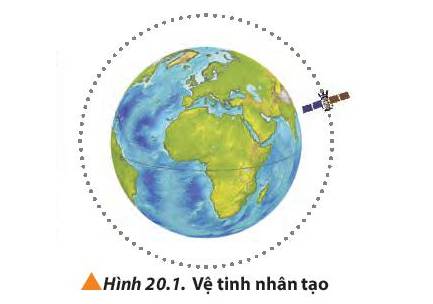
Đổi \({200^0} = \frac{{200.\pi }}{{180}} = \frac{{10\pi }}{9}(radian)\)
=> Chiều dài của cung tròn là: \(s = \alpha .R = {200^0} = \frac{{10\pi }}{9}.1,2 \approx 4,2(m)\)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Đổi \({200^0} = \frac{{200.\pi }}{{180}} = \frac{{10\pi }}{9}(radian)\)
=> Chiều dài của cung tròn là: \(s = \alpha .R = {200^0} = \frac{{10\pi }}{9}.1,2 \approx 4,2(m)\)
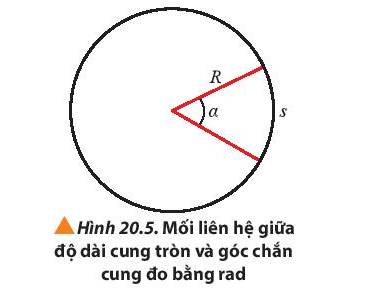
Ta cần lưu ý gì khi sử dụng công thức (20.2) để tính độ lớn của một góc chắn cung tròn có chiều dài s.
Khi cánh quạt quay, mọi điểm trên cánh quạt đều quét một cung tròn (Hình 20.2). ta có thể tính trực tiếp chiều dài cung tròn này nếu biết được góc quét bởi cánh quạt không?
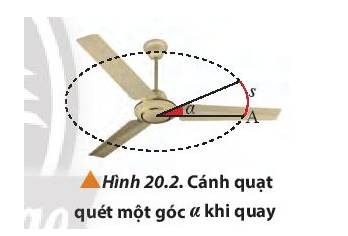
Nêu công thức tính chiều dài cung tròn s mà các em đã được học. Trong công thức này, đơn vị của góc là gì? Hãy đề xuất công thức tính chiều dài cung tròn trực tiếp và đơn giản hơn.
Trong chuyển động tròn đều, tốc độ của vật là không đổi. Vậy, chuyển động tròn đều có gia tốc không?
Trong hệ thống GPS (hệ thống định vị toàn cầu), mỗi vệ tinh nhân tạo quay xung quanh Trái Đất được hai vòng trong một giây, có độ cao khoảng 20 200 km so với mặt đất. Tính tốc độ và gia tốc hướng tâm của mỗi vệ tinh. Cho bán kính của Trái Đất bằng 6400 km.
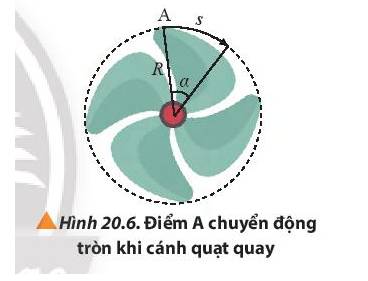
Khi cánh quạt trần quay một góc α, điểm A trên cánh quạt đi quãng đường s dài bằng bao nhiêu (Hình 20.6)?
Các vệ tinh của hệ thống GPS (hệ thống định vị toán cầu) (Hình 20.9) quay một vòng quanh Trái Đất sau một thời gian 12 giờ (gọi là chu kì). Hãy xác định tốc độ góc của các vệ tinh này.

Hãy suy ra gia tốc hướng tâm của một điểm ở chính giữa một nan hoa xe đạp trong ví dụ trên. Từ đó, có thể suy ra điều gì?
Quỹ đạo của vệ tinh nhân tạo của Trái Đất (Hình 20.1) có hình dạng gì? Tốc độ chuyển động của vệ tinh có phụ thuộc độ cao của vệ tinh đối với Trái Đất hay không?