Câu 17. Sắp xếp các số nguyên: theo thứ tự tăng dần là: Câu 18. Số nguyên đứng liền trước số đối của số 3 là:A. 2 B. -2 C. -4 D. 4 Câu 19. Kết quả phép tính: là: B. 16 C. -4 D. 4 Câu 20. Số x thỏa mãn là:A. 14 B. -14 C. 6 D. -6Câu 21. Giá trị của hiệu: là:A. 1190 B. -340 C. 340 D. 0Câu 22. Các bội của 4 lớn hơn và nhỏ hơn 12 là: C. 0;4;8 D. Câu 23. Thực hiện phép tính ta được:1 B. 9 C.- 9 D. Câu 24. So sán...
Đọc tiếp
Câu 17. Sắp xếp các số nguyên: 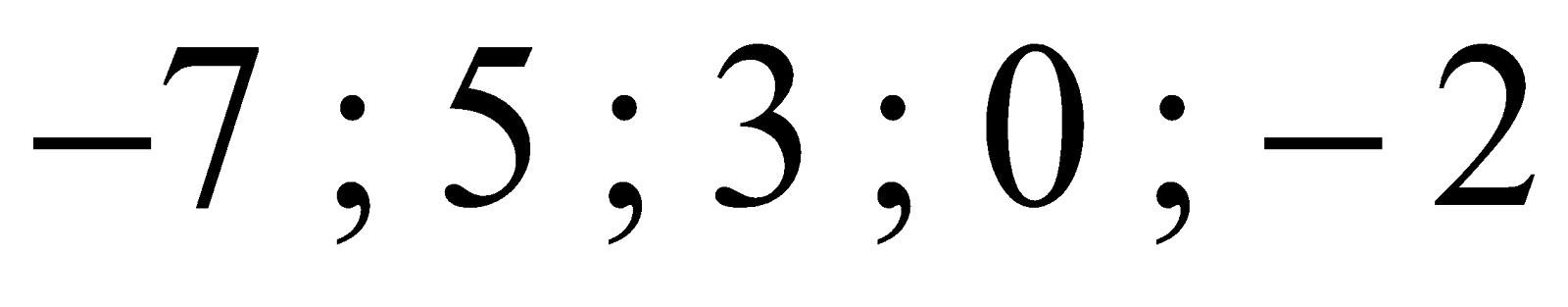 theo thứ tự tăng dần là:
theo thứ tự tăng dần là:
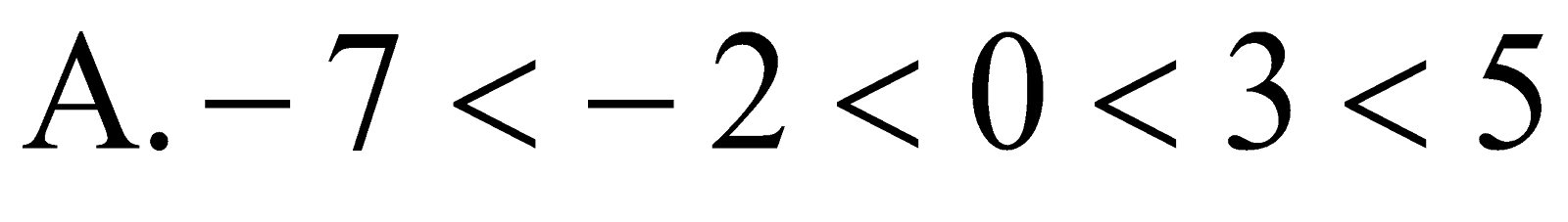
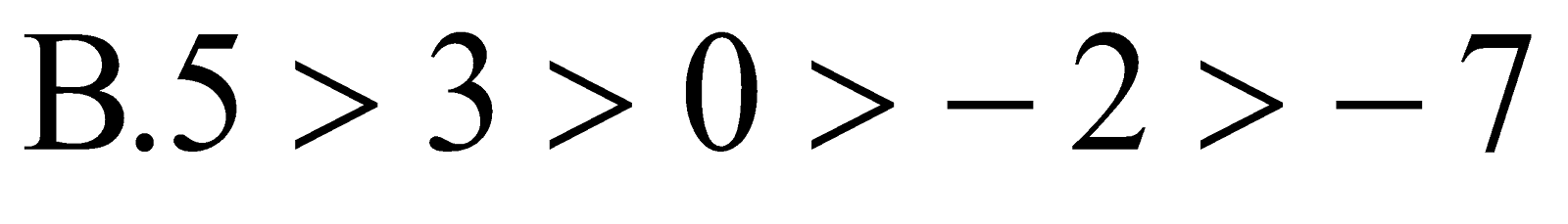
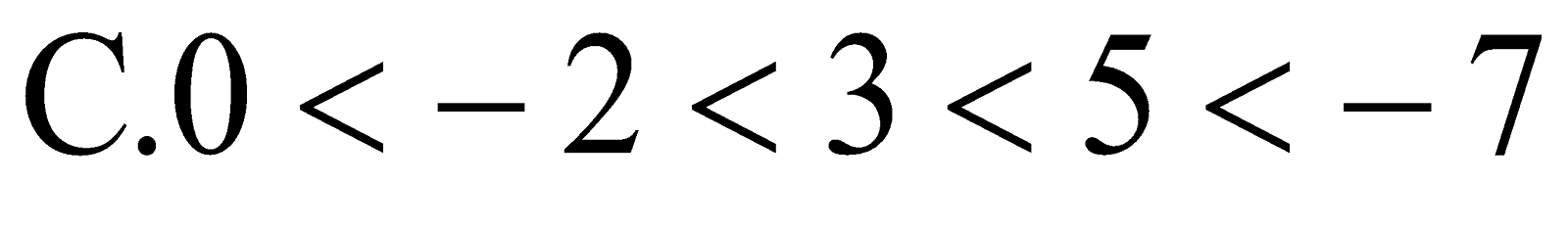

Câu 18. Số nguyên đứng liền trước số đối của số 3 là:
A. 2 B. -2 C. -4 D. 4
Câu 19. Kết quả phép tính:  là:
là:
 B. 16 C. -4 D. 4
B. 16 C. -4 D. 4
Câu 20. Số x thỏa mãn 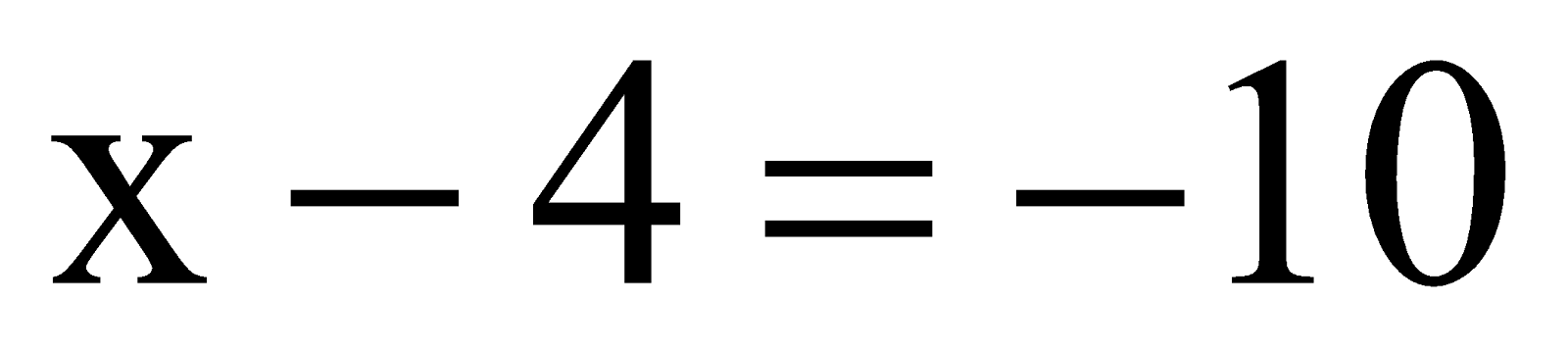 là:
là:
A. 14 B. -14 C. 6 D. -6
Câu 21. Giá trị của hiệu: 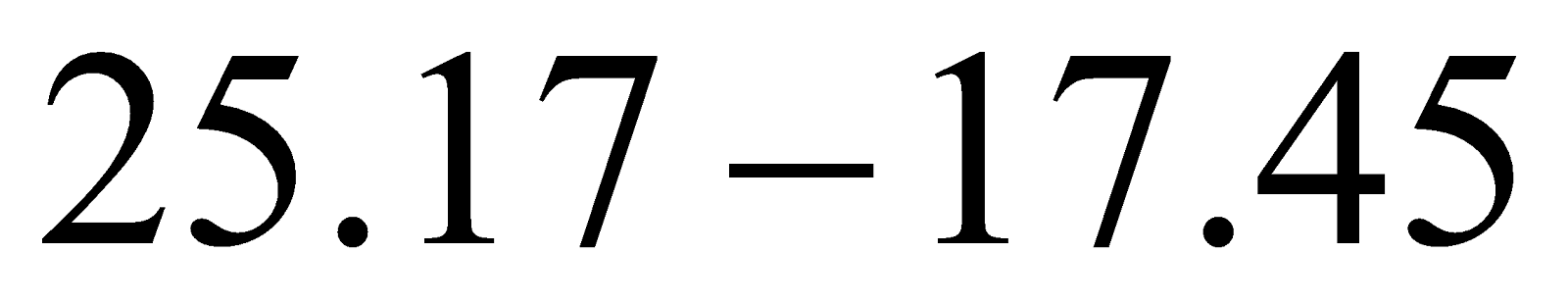 là:
là:
A. 1190 B. -340 C. 340 D. 0
Câu 22. Các bội của 4 lớn hơn  và nhỏ hơn 12 là:
và nhỏ hơn 12 là:
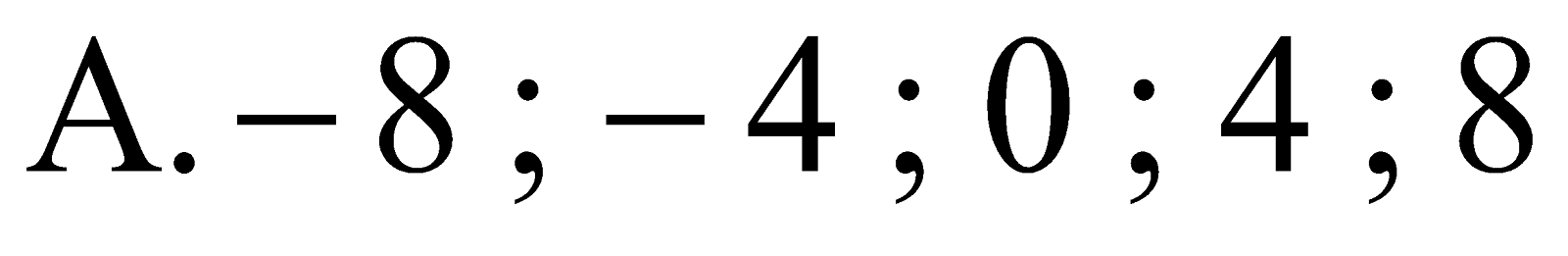
 C. 0;4;8 D.
C. 0;4;8 D. 
Câu 23. Thực hiện phép tính 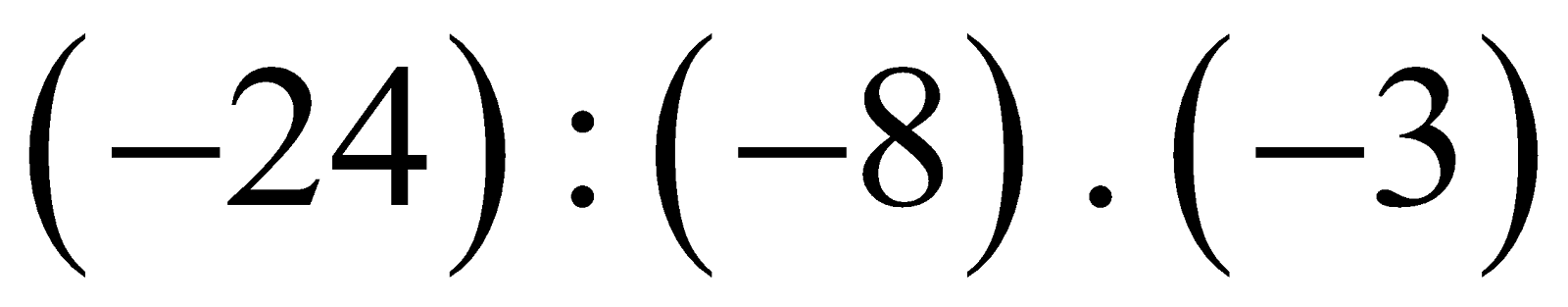 ta được:
ta được:
1 B. 9 C.- 9 D. 
Câu 24. So sánh ba số nguyên: 0 ; 3 và 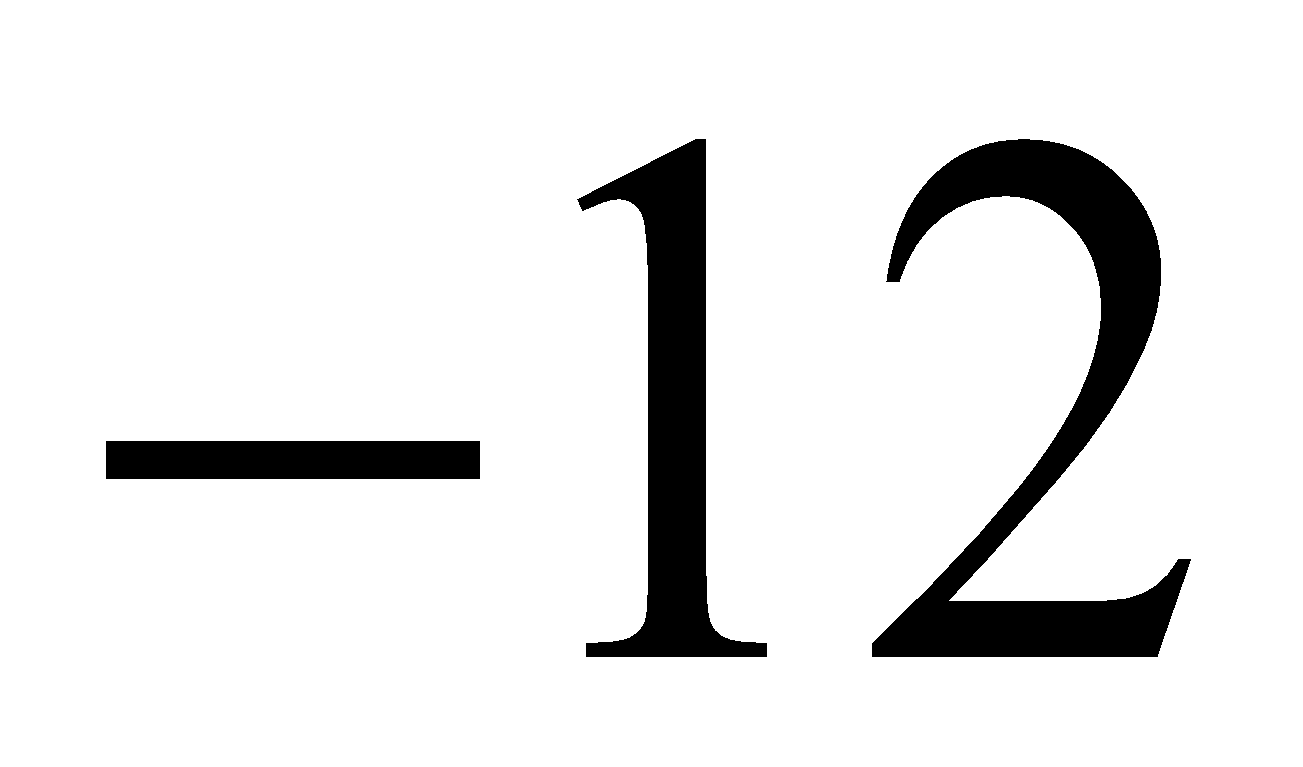 có kết quả là:
có kết quả là:

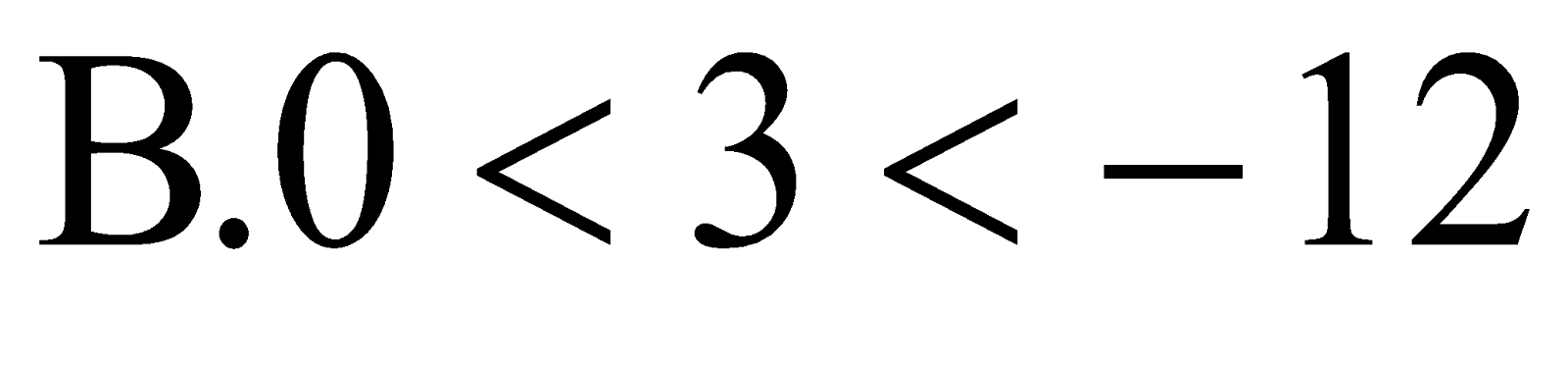


Câu 25. Trong hình lục giác đều thì:
A. Các góc bằng nhau và bằng 600. B. Các góc bằng nhau và bằng 900.
C. Đường chéo chính bằng đường chéo phụ. D. Các đường chéo chính bằng nhau.
Câu 26. Trong các hình dưới đây, hình nào là hình thang cân ?
(1) (2) (3) (4)
A. Hình 1 B. Hình 2 C. Hình 3 D.Hì

